今回は電波伝搬について解説します。 アマチュア無線をやっている人などは肌感覚として身についている人も多いかもしれません。 無線従事者試験で必ず出題される電波伝搬について紹介します。
伝搬の分類
電波はいろいろな経路で伝搬します。 電波の伝搬に仕方は地上波と上空波に分類されます。 地上波は文字通り地上を伝搬して受信点まで到達する電波です。 上空波は上空の電離層で反射や散乱して受信点に到達する電波です。
伝搬の分類と経路の模式図を下図に示します。
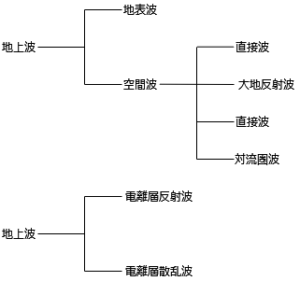

それぞれ見ていきましょう
地上波
地上波は空間を伝搬して受信点に到達する電波です。 地上波は地表波と空間波に大別されます。 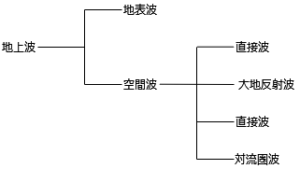
地表波
地表波は大地の不完全導体としての性質や地表による回折による影響を受けた伝搬です。 地球は球体なので地表面は湾曲しています。 この湾曲に沿って回折しながら伝搬するのが地表波です。
地表波の特徴として次のものがあります。
- 周波数が低いほど直進性が低いので減衰が少ない
- 垂直偏波のほうが水平偏波と比べて減衰が少ない
- 大地の電気伝導率が高いほど減衰が少ない(海の方が陸上より減衰が少ない)
- 低い周波数のほうが送受信点が高くても地表波による伝搬が起きやすい
地表波が効いてくるのはVHF以下くらいの周波数の電波です。
空間波
空間波はさらに直接波、大地反射波、回折は、対流圏波の4つに分類されます。 VHF以上の高い周波数の電波は電離層で反射されず突き抜けてしまい、また、地表波もほとんど減衰してしまうためおもな伝搬は空間波によるものです。
直接波
直接波は送信点から直接届く電波です。 送信点と受信点の間が自由空間であれば受信点で受信されるのはこの伝播で伝わった電波だけです。 このようなときにはフリスの公式が成り立ちます。 VHF以上の見通し範囲内の伝搬はこの伝播と大地反射波を考えれば概ね予想できます。
大地反射波
大地反射波は大地を反射して伝搬する電波です。 直接波と大地反射波が干渉する現象も起きます。 VHF以上の高い周波数では直接波と大地反射波の2つを考えれば良い近似でフリスの公式を使って伝搬距離を計算できます。
反射係数は偏波面と入射角によって変化します。 反射係数は一般に\(Re^{-j\phi}\)です。 入射波\(E_I\exp(-j\omega t)\)、反射波\(E_O\exp(-j\omega t -\phi)\)と反射したときに位相が\(\phi\)ずれたと考えれば反射係数は\(\frac{E_O}{E_I}e^{-j\phi}\)と理解できるでしょう。 水平偏波では入射角が小さくなるにつれてRは少しずつ減少し、\(\phi\)は180°で一定です。Rは入射角0°でも0.8程度です。 垂直偏波では入射角の変化によってRが大きな変化をします。 入射角が90°から小さくなるとRが急激に減少し最小値になります。 最小値となる入射角をブルースター角といいます。 \(\phi\)は入射角が90°付近で急激に上昇し入射角が90°で\(\phi=180\)°となります。
回折波
回折波は山などの特にナイフエッジ状の紹介物により回折した電波です。 回折波と直接受信点に届く電波とが干渉する領域があります。 この領域をフレネルゾーンといいます。
対流圏波
大気の場所によって状態が変化するため誘電率が変化します。 誘電率が違えば屈折率が異なるため、電波は直進せず湾曲した経路を通ります。 このような伝搬を対流圏波と呼びます。
これらの伝搬の他にもダクトなどいろいろな要因で面白い伝搬をすることがあります。
上空波
上空波は上空にある電離層経由で受信点に到達する電波です。 電離層は太陽をはじめとした宇宙からの紫外線や荷電粒子の影響で大気が電子と陽イオンに電離した領域です。 電離層ではHF以下の低い周波数の電波が反射されます。

電離層
電離層にはいくつか種類があり、地表からの距離によって次のように分類されます。
- D層:50km~
- E層:約100km
- \(F_1\)層:約200km
- \(F_2\)層:約400km
地表に近い領域ほど電離度が低く低い周波数が反射されます。E層ではLF,MF、F層ではHFです。 太陽からの影響が時間によって変わるのでこれらの電離層の高度も時間によって変化します。 初夏の時期に100km付近にスポラジックE層と呼ばれる層が出現することがあります。 100MHz以下のVHFが反射されます。
電離層反射波
電離層は電離層での反射されて地上の受信点に到達する電波です。 見通し距離外へ伝搬するのでHFなどで海外との通信などに使われます。
電離層散乱波
こちらは電離層で散乱した電波です。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人
次回予告
特殊な伝搬や電離層での反射の原理的なところを解説したいと思います。
前回
次回
近日中
本シリーズについて
勉強法


コメント