【過去問解説】令和5年7月の1陸技試験問題を解いてみた（R5.7 2回目無線工学A A-1~A-5）

令和5年7月の1陸技の試験2回目の無線工学AのA-1～5の問題について解説します。

R.5.7 無線工学A（2回目） A-1
1. A
2. B
3. C
R.5.7 無線工学A（2回目） A-2
R.5.7 無線工学A（2回目） A-3
R.5.7 無線工学A（2回目） A-4
R.5.7 無線工学A（2回目） A-5
1. A
2. B
3. C
まとめ
参考文献

R.5.7 無線工学A（2回目） A-1

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学A A-1

地上系デジタル放送の標準方式(ISDB-T)に関する問題です。

A

地上系デジタル放送では時間方向では4シンボル、周波数方向では3シンボルごとにパイロット信号SPが挿入されます。

全体では12シンボルに1つ挿入される計算になります。

そのため、Aには「12」が入ります。

B

OFDMはSP1つとデータシンボル11個が繰り返されていると考えることができるので、全体の平均電力はSPごとの平均電力を計算すれば問題ありません。

$N_p$データシンボルごとに1データシンボル$L^2C_D$の電力でそれ以外のデータシンボルの平均電力は$C_D$なのでここから$C_A$を計算できます。 \[ C_A=\frac{L^2+N_p-1}{N_p}C_D \] となります。

$C_D/C_A$は \[ C_D/C_A=\frac{N_p}{L^2+N_p-1} \] となります。

そのため、Bには「$\frac{N_p}{L^2+N_p-1}$」が入ります。

C

Bの結果に$L=4/3$、$N_p=12$を代入すると \[ C_D/C_A=0.939\simeq 0.94 \]

そのため、Cには「0.94」が入ります。

以上から答えは5です。

R.5.7 無線工学A（2回目） A-2

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学A A-2

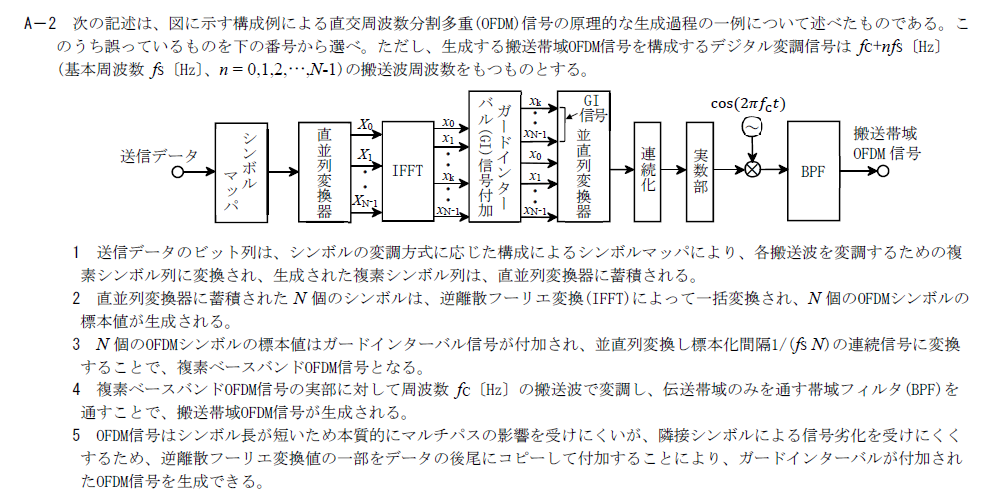
OFDMの原理に関して誤った選択肢を選ぶ問題です。

同様の問題が令和4年1月1回目A-1で出題されています。

下記の記事もご参照ください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学A A-1~A-5）

１陸技令和4年1月の無線工学A(1回目)の問題を解いてみました。今回はA-1~5です。

誤った選択肢は5です。

OFDMはシンボル長が長いため本質的にマルチパスの影響を受けにくいです。

そのため、5の前半部分が誤りで答えは5です。

R.5.7 無線工学A（2回目） A-3

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学A A-3

AMの変調波の側波帯電力を計算する問題です。

この問題は同様の問題が令和3年7月1回目A-3で出題されています。

計算方法については下記の記事をご参照ください。

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 1回目　無線工学A A-1~A-5）

１陸技令和3年7月の無線工学Aの問題を解いてみました。今回は第1回A-1~5を解きました。

上記の記事の式に当てはめると \[ \frac{m^2}{2(2+m^2)}P=\frac{0.8^2}{2(2+0.8^2)}\times 330=40\rm{[W]} \] となります。

以上から答えは3です。

R.5.7 無線工学A（2回目） A-4

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学A A-4

受信機入力のC/Nから送信機の送信電力を求める計算問題です。

この問題は同様の問題が令和4年1月1回目A-8で出題されています。デシベルと真数が混ざっていてこちらの問題の方が面倒くさいので気を付けましょう。

下記の記事もご参照ください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学A A-6~A-10）

１陸技令和4年1月の無線工学A(1回目)の問題を解いてみました。今回はA-6~10です。

ボルツマン係数や周囲温度をデシベルに直すのは骨が折れる一方で受信機入力まではデシベルで記述されています。そのため、まず受信機入力までをデシベルで計算、この結果を真数に直して進数で$C/N$を計算した後にデシベルに直し、求めるべき$P$を計算することにします。

まず、受信機入力電力を$P_r\rm{[dBW]}, P_R\rm{[W]}$、雑音電力を$N\rm{W}$とすると \[ P_r=10\log P -4+40-140+40-4 \\ =10\log P -48 \] となり、真数に直すと \[ P_R=10^{\frac{P_r}{10}}=P \times 10^{-6.8} \] です。

一方で雑音電力を計算すると \[ N=FkTB \\ =2.5 \times 1.38 \times 10^{-23}\times 290 \times 20 \times 10^6 \\ =2.001 \times 10^{-13} \simeq 2\times 10^{-13} \rm{[W]} \] です。

$C/N$を計算すると \[ C/N=P_R/N=P/2 \times 10^{6.2} \] なので \[ 10\log (C/N)=10 \log P -3 +62=10\log P +59 \] となります。

問題文から \[ 10\log (C/N)=65 \] なので、計算すると \[ 10\log P=6\\ P=4 \rm{[W]} \] となります。

以上から答えは4です。

R.5.7 無線工学A（2回目） A-5

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学A A-5

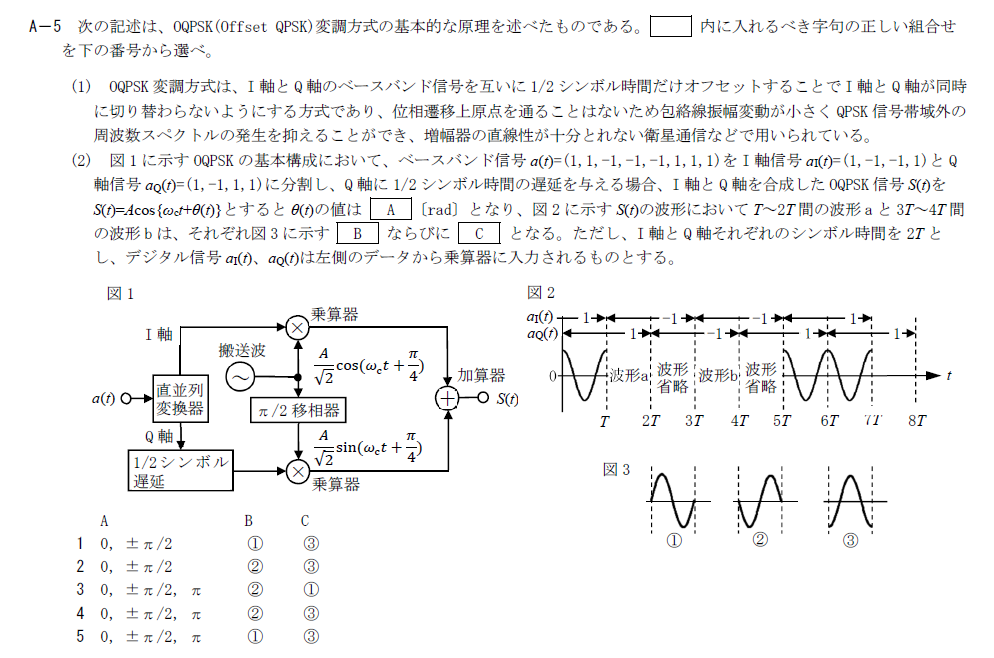
OQPSKの原理に関する問題です。

A

OQPSKはQPSKの位相をオフセットして、信号の位相が$0,\pm \pi /2,\pi$をとるようにした変調方式です。 QPSKでは$\pm \pi /4,\pm 3\pi /4$のいずれかをとります。

ここまでの説明からAには$0,\pm \pi /2,\pi$が入ります。

そもそも$0,\pm \pi /2$では位相が3値しかありません。

B

BとCの空欄では図1の出力を実際に計算します。。

Bには波形aに相当する波形を計算します。この時、$a_I(t)=-1,a_Q(t)=1$なので、 \[ S(t)=\frac{A}{\sqrt{2}}\left\{-\cos \left( \omega_c t +\frac{\pi}{4}\right)+\sin \left( \omega_c t +\frac{\pi}{4}\right)\right\} \\ =\frac{A}{\sqrt{2}}\left\{-\cos\omega_ct\cos\frac{\pi}{4}+\sin\omega_ct\sin\frac{\pi}{4}+\sin\omega_ct\cos\frac{\pi}{4}+\cos\omega_ct\sin\frac{\pi}{4}\right\} \\ =A\sin \omega_ct \] となります。

$A\sin \omega_ct$の波形なのは①です。

そのため、Bには①が入ります。

C

\[ S(t)=\frac{A}{\sqrt{2}}\left\{-\cos \left( \omega_c t +\frac{\pi}{4}\right)-\sin \left( \omega_c t +\frac{\pi}{4}\right)\right\} \\ =\frac{A}{\sqrt{2}}\left\{-\cos\omega_ct\cos\frac{\pi}{4}+\sin\omega_ct\sin\frac{\pi}{4}-\sin\omega_ct\cos\frac{\pi}{4}-\cos\omega_ct\sin\frac{\pi}{4}\right\} \\ =-A\cos \omega_ct \]

$-A\cos \omega_c$の波形なのはなのでCには③が入ります。。

以上から答えは5です。