令和6年1月の一陸技の試験の無線工学BのA-6~10の問題について解説します。
R.6.7 無線工学B A-6

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-6
平行二線式線路の減衰定数を求める問題です。 公式を使うことで簡単に求められます。
ここではまず公式を使って計算をして、その後詳しく知りたい方のために公式を導出します。
減衰定数は問題文の条件$Rgg \omega L,G=0$の条件では \[ \alpha = \frac{R}{2Z_0} \] となります。 $Z_0$は特性インピーダンスです。 $R$は問題文に与えられた$R_0$が導線1本分なので平行二線式線路では$R=2R_0$となります。
計算すると \[ \alpha =\frac{2R_0}{2Z_0}=\frac{0.0832\sqrt{f}}{dZ_0} \\ =9.24 \times 10^{-4} \rm{[Np/m]} \\ =8.03 \times 10^{-3} \rm{[dB/m]} \] となります。
以上から答えは4です。
ここからは公式を導出します。 不要な方は読み飛ばしてください。
単位長さあたりの等価回路は下図のようになります。
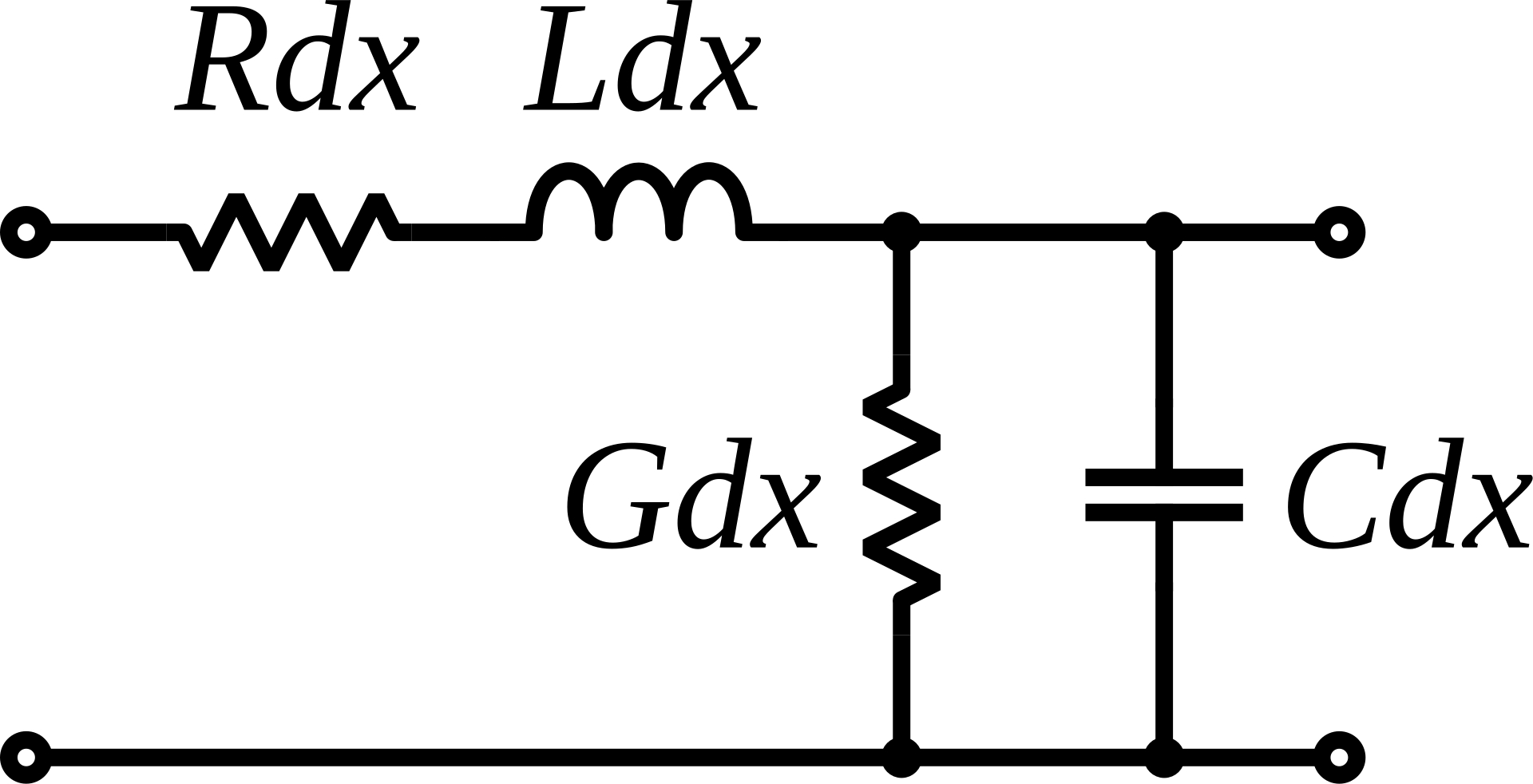
ここで \[ Y=G+j\omega C \\ Z=R+j\omega L \] と置くと \[ dV=IZdx \\ dI=VYdx \] となります。
この2式を変形して \[ \frac{dV}{dx}=IZ \\ \frac{dI}{dx}=VY \] となります。
さらに$x$で微分すると \[ \frac{d^2V}{dx^2}=Z\frac{dI}{dx}=YZV \\ \frac{d^2I}{dx^2}=Y\frac{dV}{dx} =YZI \] となります。
2階の線形微分方程式なので$V=e^{\lambda x}$と置くと \[ \lambda^2-YZ=0 \\ \lambda=\pm \sqrt{YZ} \] が成立します。 ここで \[ \gamma =\sqrt{YZ}と置きます。 \]
$\gamma$は伝搬定数です。
一般解はこれらの線形結合でかけるので \[ V=A_1e^{\gamma x}+A_2e^{-\gamma x} \] と表せます。
$x=0$の時、$V=V_0,I=I_0$として \[ \frac{d^2V}{dx^2}=YZV \\ \frac{dV}{dx}=IZ \] にそれぞれ代入すると \[ V_0=A_1+A_2 \\ I_0Z=A_1\gamma -A_2\gamma \] なので、 \[ A_1=\frac{V_0+I_0Z_0}{2} \\ A_2=\frac{V_0-I_0Z_0}{2} \] です。 ここで、 \[ Z_0=\sqrt{\frac{Z}{Y}} \] となります。
$Z_0$は特性インピーダンスです。
伝搬定数を \[ \gamma =\alpha +j\beta \] と実部と虚部に分けて書けます。 $\alpha$は減衰定数、$\beta$は位相定数と呼ばれています。
$R \gg \omega L,G \gg \omega C$の時、下記が成立します。 \[ \gamma =\sqrt{(R+j\omega L)(G+j\omega C)} \\ =\sqrt{-\omega^2 LC\left(\frac{R}{j\omega L}+1\right)\left(\frac{G}{j\omega C}+1\right)} \\ =\sqrt{-\omega^2 LC\left(-\frac{RG}{\omega^2LC}+\frac{R}{j\omega L}+\frac{G}{j\omega C}+1\right)} \\ \simeq j\omega \sqrt{LC}\left(1-j\frac{R}{2\omega L}-j\frac{G}{2\omega C}\right) \] ここから \[ \alpha =\frac{R}{2}\sqrt{\frac{C}{L}}+\frac{G}{2}\sqrt{\frac{L}{C}} \\ \beta =\omega \sqrt{LC} \] です。
$\alpha$の第一項は導体損失、第二項は誘電体損失です。
同じ条件で特性インピーダンスは \[ Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}\simeq \sqrt{\frac{L}{C}} \] です。
R.6.7 無線工学B A-7
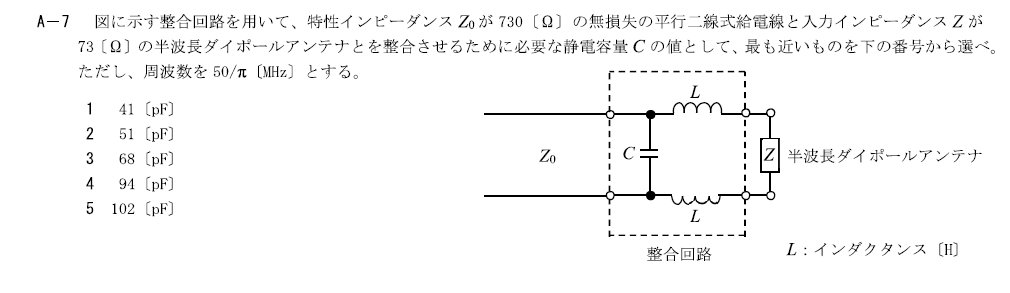
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-7
整合回路に関する問題です。
この問題は同様の問題が令和6年1月A-7や令和4年1月1回目A-9で出題されています。 値が違うだけなので計算方法は下記をご参照ください。
令和4年1月1回目A-9

令和6年1月A-7

問題の値を使って計算すると \[ C=\frac{1}{2\pi \times 50/\pi \times 730 \times 10^6}\sqrt{\frac{730-73}{73}}=\frac{3}{730\times 10^8} \\ =4.11 \times 10^{-11}\rm{[F]}=41\rm{[pF]} \] で答えは1です。
R.6.7 無線工学B A-8
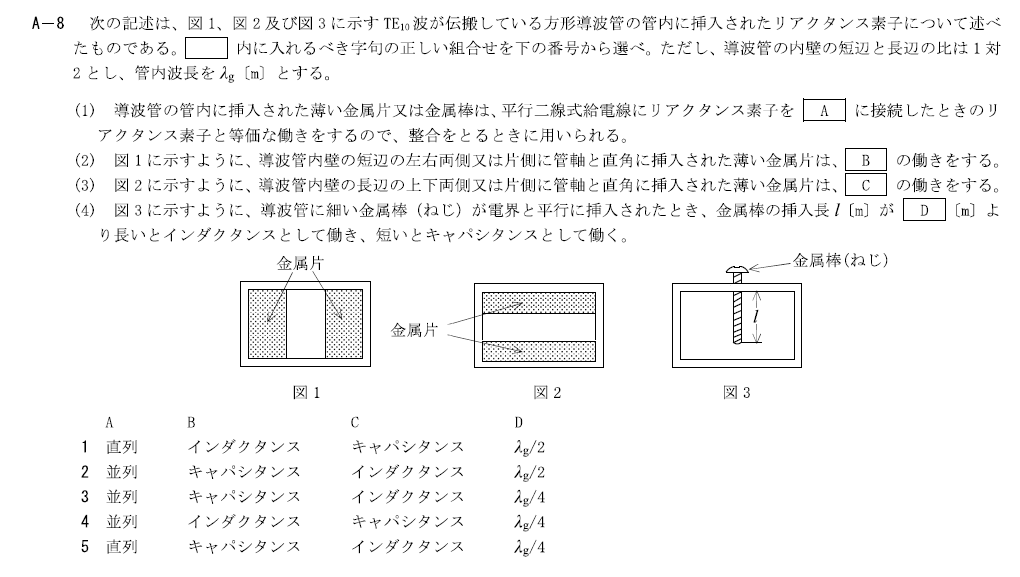
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-8
導波管に金属片を挿入した時の動作に関する問題です。
この問題は同様の問題が令和4年7月1回目A-9で出題されています。 (2)と(3)が入れ替わっているだけです。
下記の記事をご参照ください。

答えは
- A:並列
- B:インダクタンス
- C:キャパシタンス
- D:$\lambda_g/4$
で、4です。
R.6.7 無線工学B A-9

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-9
給電線とアンテナが整合してないときの伝送効率に関する計算問題です。
この問題は全く同じ問題が令和4年7月2回目A-9で出題されています。
詳細は下記の記事をご参照ください。

答えは
- A:$-2al$
- B:$P_{\rm{RA}}|\Gamma |^2$
- C:$\eta_0\frac{1-|\Gamma|^2}{1-|\Gamma |^2\eta_0^2}$
- D:$\lambda_g/4$
で、3です。
R.6.7 無線工学B A-10

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-10
逆L型接地アンテナの水平部と垂直部の長さを計算する問題です。
この問題は同様の問題が令和5年1月1回目A-10で出題されています。
下記の記事をご参照ください。

実効長$l_e$は垂直部の長さと等しく$l_e=l_2$なので、 \[ Il_e=20 \\ l_e=\frac{20}{I}=5\rm{[m]} \] となり、 \[ l_2=5\rm{[m]} \]
この結果から \[ l_1+l_2=15 \\ l_1=10 \rm{[,]} \] です。
以上から答えは2です。
まとめ
今回は令和6年7月の無線工学Bの試験A-6~A-10の問題について解説しました。 A-6については過去にあまり出題されていないタイプの問題でした。 公式を覚えていないとすぐに計算できず、最初の方に出題されているので分からなければ飛ばして後回しにしましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント