令和5年1月の1陸技の試験1回目の無線工学BのA-16~20の問題について解説します。
R.5.1 無線工学B(1回目) A-16

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学B A-16
F層1回反射により受信した電界強度から第2種減衰を計算する問題です。
同様のシチュエーションで受信電界強度を計算する問題が令和4年1月1回目のA-16で出題されています。
計算の方針として、減衰をなしとして計算した電界強度から実際に受信した電界強度を引くことで第2種減衰を求めます。
伝搬距離$d$は$d=2\times \sqrt{400^2+300^2}=1000\rm{[km]}$です。
半波長ダイポールアンテナから距離$d$離れた受信点の電界強度$E$は \[ E=\frac{7\sqrt{P}}{d} \] です。 ここで$P$は放射電力です。
これに問題の値を代入すると \[ E=\frac{7\times\sqrt{4900}}{1000} \\ =49 \times 10^{-5}\rm{[V/m]} \\ =490\rm{[\mu V/m]} \] です。
単位を$\rm{dB\mu V/m}$に直すと \[ E=20\log 490 =54\rm{[dB\mu V/m]} \] です。
実際に受信された電界強度は$48[\rm{dB\mu V/m}]$なので、差の$6[\rm{dB}]$が第2種減衰量となります。
以上から答えは2です。
R.5.1 無線工学B(1回目) A-17

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学B A-17
球面大地での電波伝搬を求める問題です。
値が違う同様の問題が令和4年1月2回目のA-17で出題されています。 また、計算方法について誘導がついた類似問題が令和3年1月の1回目A-14で出題されています。
それぞれ下記記事をご参照ください。


実際に計算すると \[ h=\frac{d^2}{2KR}=0.0529\rm{[km]} \\ =53\rm{[m]} \] です。
以上から、答えは4です。
R.5.1 無線工学B(1回目) A-18
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学B A-15
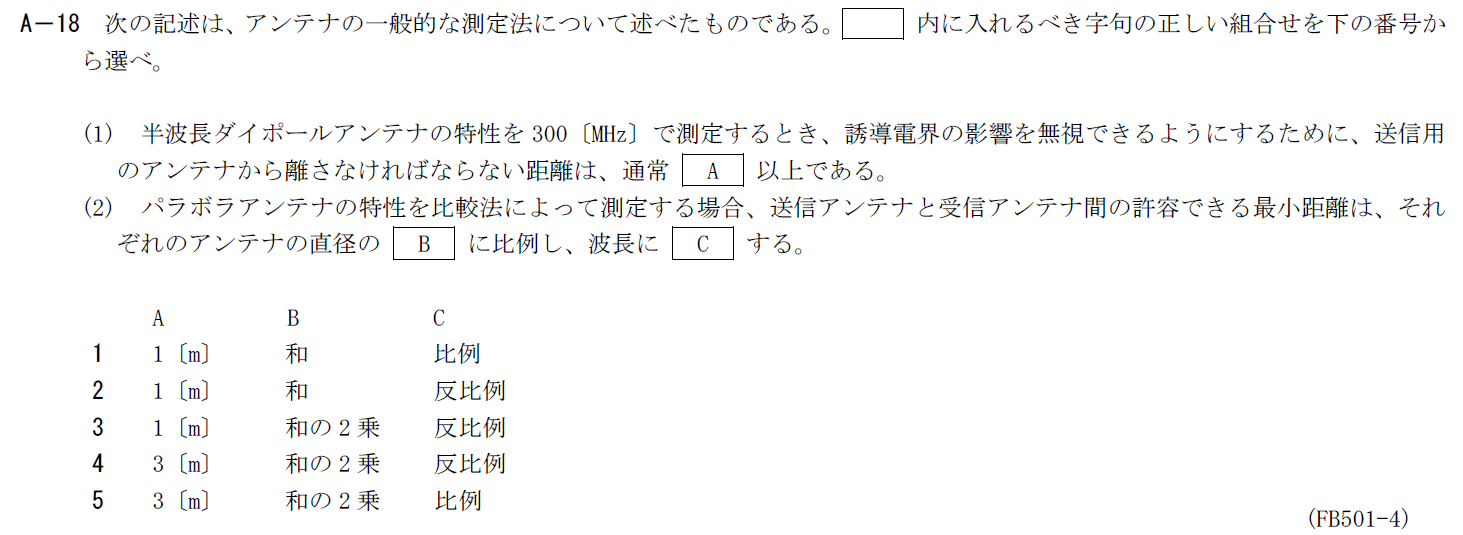
アンテナの測定方法に関する問題です。
A
誘導電界の影響を無視するためには波長より十分な距離を離す必要があります。
一般には3波長以上が必要なので、300MHzの3波長分の3[m]が入ります。
B,C
(2)はパラボラアンテナの特性を測定する時の送受信アンテナ間の距離に関して記載されています。 アンテナ近傍では静電界や誘導電磁界の影響を受けやすく、アンテナ本来の特性をうまく測定することができません。 近傍の領域をフレネル領域、それより遠方の領域をフラウンホーファ領域といいます。
パラボラアンテナのような開口アンテナではこれらの領域の境界までの距離$d$は、波長を$\lambda$、アンテナの直径を$D$として \[ d=\frac{2D^2}{\lambda} \] となります。
送受信アンテナ同士はフラウンホーファ領域ない煮なければならないため、上記の距離が最小距離となります。
以上からBは「和の2乗」、Cは「反比例」です。 その結果、答えは4です。
R.5.1 無線工学B(1回目) A-19

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学B A-19
ハイトパターンの測定に関する問題です
この問題は令和3年1月1回目のA-19と全く同じ問題です。 下記の記事をご参照ください。

また、類似問題が令和4年7月1回目のA-19で出題されています。 下記の記事も参考にしてください。

答えは4です。
R.5.1 無線工学B(1回目) A-20

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年1月1回目 無線工学B A-20
反射板を用いたアンテナ利得の測定に関する問題です。
似たようなシチュエーションの問題が令和3年7月2回目のA-19で出題されています。 下記の記事も参考にしてください。

A
アンテナから反射板までの往復分の伝搬距離に対してフリスの公式を適用します。
$P_r$を計算すると \[ P_r=\frac{G}{4\pi (2d)^2}P_t\frac{\lambda^2}{4\pi}G \\ =\frac{G\lambda^2}{4\pi}\frac{P_tG}{16\pi d^2} \] となります。
そのため、Aには「$\frac{P_tG}{16\pi d^2}$」が入ります。
B
$P_r/P_t$と$S$の関係を考えるために、まずは電圧反射係数を考えましょう。
電圧反射係数$\Gamma$は入力電圧と反射電圧の比なので、次の関係が成り立ちます。 \[ |\Gamma|=\sqrt{P_r/P_t} \]
次に電圧反射係数を電圧定在波比で表します。 \[ S=\frac{1+|\Gamma_V|}{1-|\Gamma_V|} \] なので、$\Gamma$について解くと \[ |\gamma|=\frac{1-S}{1+S} \] です。
最初の式に代入すると \[ \frac{P_r}{P_t}=\left( \frac{1-S}{1+S}\right)^2 \] となるので、Bには$\frac{1-S}{1+S}$が入ります。
C
①の式を$G$について解くと \[ G=\frac{8\pi d}{\lambda}\sqrt{\frac{P_r}{P_t}} \] です。
$\sqrt{\frac{P_r}{P_t}}$がBの内容なので、Cには「$\frac{8\pi d}{\lambda}$」が入ります。
以上から答えは3です。
まとめ
今回は令和5年1月の無線工学B(1回目)の試験A-16~A-20の問題について解説しました。 A問題の後半は特に計算問題が多いので、公式まで暗記する必要はありませんが、計算過程を理解して応用できるようにしておくことが重要です。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント
A-17の問題ですが、h=d^2/2KRが正しいかと思います。(本文に分母の2がありません)
ご指摘ありがとうございます。その通りです。
修正いたしました。