令和5年7月の1陸技の試験1回目の無線工学BのA-16~20の問題について解説します。
R.5.7 無線工学B(1回目) A-16

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-16
電離層シンチレーションに関する問題です。
全く同じ問題が令和3年7月2回目A-17で出題されています。 下記の記事をご参照ください。

空欄は以下の通りです。
- A:短周期
- B:緯度
- C:直線偏波
答えは2です。
R.5.7 無線工学B(1回目) A-17

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-17
太陽フレアに関する問題です。 ここ最近ではあまり出題されていないタイプの問題です。
A
この空欄については問題がよくないです。 ミリ波、X線ともに電磁波で太陽フレアによって特定の周波数のみが放射されるわけではないため、絞ることができません。
B~Dで答えを絞ることができますのでここはいったん無視しましょう。
B
太陽フレア後、太陽から最初に地球に到達するのは光の速さで伝搬する電磁波です。
太陽から地球の距離は約1億5000万[km]、つまり$1.5 \times 10^{11}\rm{[m]}$で光の速さが$3\times 10^8 \rm{[m/s]}$です。 そのため、太陽から出た光が地球に到達するまで約500秒=8.3分かかります。
このことからBには「8分」が入ります。
割と有名なので覚えている人もいるかもしれません。 2秒はおおよそ地球と月の間を光が往復する時間です。
C
太陽活動の周期はおよそ11年周期で変動しているといわれています。
そのため、Cには「11年」が入ります。
D
太陽フレアなどにより高エネルギーの陽子が増加する現象はプロトン現象と呼ばれています。 プロトンは英語で陽子の事です。
そのため、Dには「プロトン」が入ります。
デリンジャ現象も太陽フレアが原因でおこる現象ですが、こちらはD層の電子密度が増加し通信障害がおこる現象です。 将来同様の問題が出題されるとき、ここの記述がデリンジャ現象になって出題されることも十分考えられます。 令和4年7月1回目A-17のようにデリンジャ現象単体で問題になることもあるので、これを機に押さえておきましょう。
B~Dの内容に合致する選択肢は3のみです。
以上から答えは3です。
R.5.7 無線工学B(1回目) A-18

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-18
ビームアンテナの指向性利得の近似計算に関する問題です。
①の式が与えられる形の計算問題が令和5年1月1回目A-3や令和3年7月1回目A-2で出題されています。
下記の記事もご参照ください。


A
空欄Aは前述の問題で問題文中に与えられていた式を答えさせる問題になっています。 過去問演習をある程度重ねた人であれば記憶に残っている人もいるかもしれません。
指向性利得は特定方向の電力密度と全放射電力を全方向に平均した値との比の事を言います。 アンテナからの距離を$r$、電界方向の角度を$d\theta_E$、磁界方向の角度を$d\theta_H$とすると立体角$d\omega$は \[ d\omega =\frac{rd\theta_E \dot rd\theta_H}{r^2}=d\theta_Ed\theta_H \] となります。
指向性利得$G_d$は立体角の比に等しく、全休の立体角は$4\pi$なので \[ G_d=\frac{4\pi}{\int d\theta_Ed\theta_H} \] となります。
電界、磁界面の半値角内にビームアンテナの全放射電力が一様に分布すると近似すると \[ \int d\theta_Ed\theta_H=\theta_E\theta_H \] となり、Aには「$\frac{4\pi}{\theta_E\theta_H}$」が入ります。
B
$\theta_1,\theta_2$を使って$\theta_E,\theta_H$を表すと \[ \theta_E=\frac{\pi}{180}\theta_1 \\ \theta_H=\frac{\pi}{180}\theta_2 \] となります。
①の式に代入すると \[ G_d=\frac{4\pi \times 180^2}{\theta_1\theta_2} \\ =\frac{41253}{\theta_1\theta_2}\simeq \frac{40000}{\theta_1\theta_2} \] です。
そのため、Bには「$\frac{40000}{\theta_1\theta_2}$」が入ります。
C
②式に問題の値を代入すると、 \[ 10\log G_d=10\log \frac{40000}{4.5 \times 4} \\ =10(4-\log\frac{9}{2})=33.4 \simeq 33\rm{[dB]} \] となります。
そのため、Cには「33」が入ります。
以上から答えは1です。
R.5.7 無線工学B(1回目) A-19
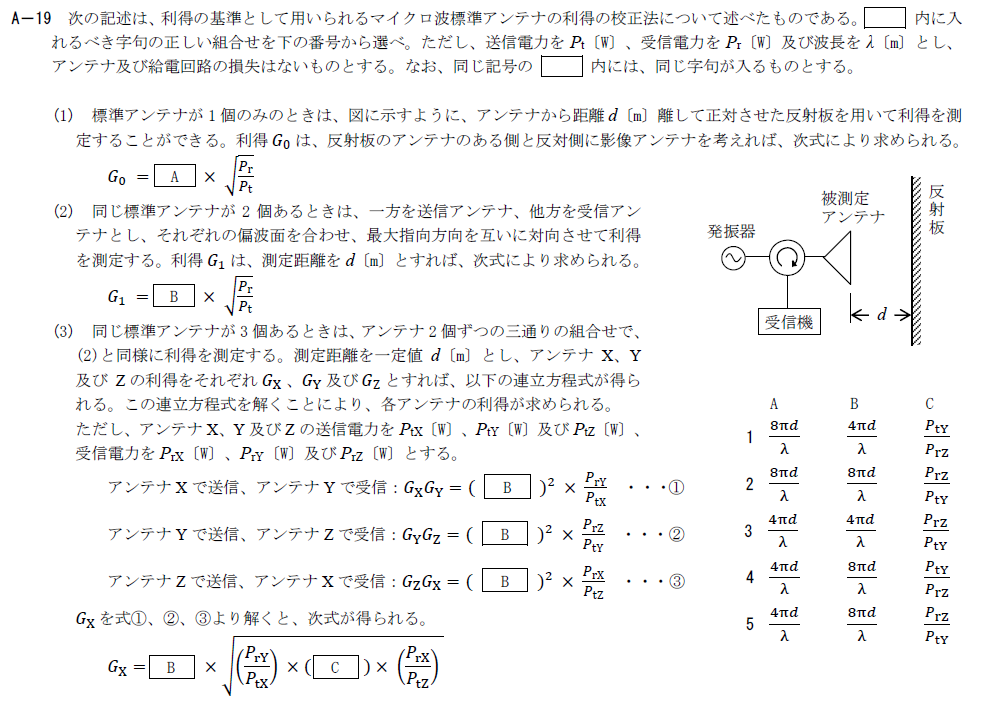
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-19
マイクロ波標準アンテナの校正法に関する問題です。
全く同じ問題が令和3年7月2回目A-19で出題されています。
下記の記事をご参照ください。

空欄に入る言葉は下記のとおりです。
- A:$\frac{8\pi d}{\lambda}$
- B:$\frac{4\pi d}{\lambda}$
- C:$\frac{P_{tY}}{P_{rZ}}$
以上から答えは1です。
R.5.7 無線工学B(1回目) A-20

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-20
マイクロ波アンテナの利得測定をするときの平面大地の反射波等の影響に対する対策に関する問題です。
A
(1)は大地による反射を防ぐための反射防止板に関する記述です。 反射防止板のエッジ部分では回折が発生しますが、ここに凹凸を設けることでこの影響を低減できます。
回折が発生するエッジ部分に凹凸を設けることで凸部で回折した回折波が凹部で遮られるため受信点に到達する回折波を弱めることができます。
そのため、Aには「凹凸」が入ります。
B
アンテナを高い位置に設置することで、大地反射波の経路を長くして減衰を大きくすることができます。 これにより、大地反射波の影響を軽減できます。
そのため、Bには「高い」が入ります。
C
ハイトパターンからは電界強度分布から大地の反射係数を求めることができます。 反射係数から計算により反射波の影響を補正することで影響を軽減できます。
そのため、Cには「反射係数」が入ります。
以上から答えは3です。
まとめ
今回は令和5年7月の無線工学B(1回目)の試験A-16~A-20の問題について解説しました。 太陽フレアなど近年あまり見ない傾向の問題や、過去問の中から複数の類題を組み合わせた難易度の高い問題が出題されています。 基本的な内容の組み合わせではあるので過去問演習で対策しておきましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント