【過去問解説】令和7年7月の1陸技試験問題を解いてみた（R7.7 無線工学B A-6~A-10）

令和7年7月の一陸技の試験の無線工学BのA-6～10の問題について解説します。

R.7.7 無線工学B A-6
R.7.7 無線工学B A-7
R.7.7 無線工学B A-8
R.7.7 無線工学B A-9
R.7.7 無線工学B A-10
まとめ
参考文献

R.7.7 無線工学B A-6

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R7年7月　無線工学B A-6

VSWRからインピーダンスを計算する問題です。

この問題は同様の問題が令和4年1月1回目A-7で出題されています。

下記の記事をご参照ください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学B A-6~A-10）

１陸技令和4年1月の無線工学B(1回目)の問題を解いてみました。今回はA-1~5です。

VSWRを$S_V$、給電線の特性インピーダンスを$Z_0$、負荷のインピーダンスを$Z_R$とすると \[ S_V=\frac{|Z_R+Z_0|+|Z_R-Z_0|}{|Z_R+Z_0|-|Z_R-Z_0|} \] となります。

$Z_R>Z_0$の時と$Z_0>Z_R$の時で結果が変わります。

$Z_R>Z_0$の時 \[ S_V=\frac{Z_R}{Z_0} \\ Z_R=S_VZ_0=62.5\rm{[\Omega]} \] $Z_0>Z_R$の時 \[ S_V=\frac{Z_0}{Z_R} \\ Z_R=\frac{Z_0}{S_V}=40\rm{[\Omega]} \] 以上から答えは1です。

R.7.7 無線工学B A-7

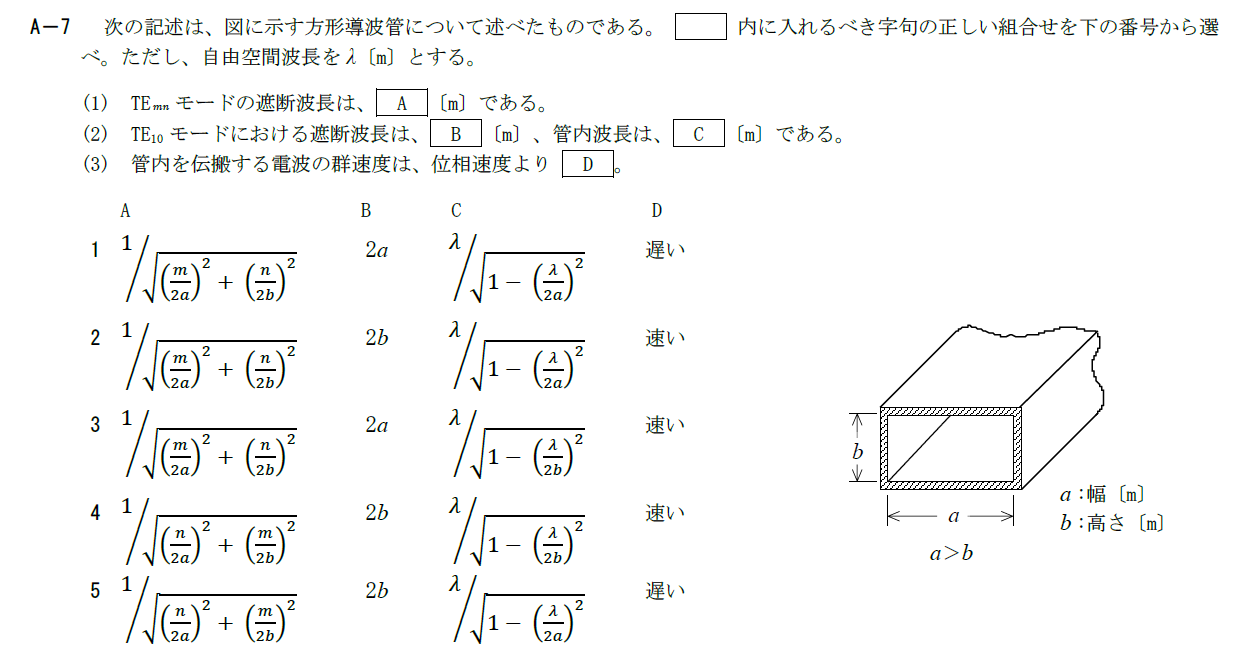
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R7年7月　無線工学B A-7

方形導波管に関する問題です。

この問題は全く同じ問題が令和5年7月2回目A-8で出題されています。また、類似問題が何度か出ています。

下記の記事をご参照ください。

【過去問解説】令和5年7月の1陸技試験問題を解いてみた（R5.7 2回目無線工学B A-6~A-10）

１陸技令和5年7月の無線工学B(2回目)の問題を解いてみました。今回はA-6~10です。

類似問題は下記の記事をご参照ください

令和4年7月2回目B-2

【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 2回目無線工学B B-1~B-5）

１陸技令和4年7月の無線工B(2回目)の問題を解いてみました。今回はB-1~5です。

令和3年7月1回目B-2

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 1回目　無線工学B B-1~B-5）

１陸技令和3年7月の無線工学Bの問題を解いてみました。今回は第1回B-1~5を解きました。

答えは

A:$\frac{1}{\sqrt{\left(\frac{m}{2a}\right)^2+\left(\frac{n}{2b}\right)^2}}$
B:$2a$
C:$\lambda_g=\frac{\lambda}{\sqrt{1-\left(\frac{\lambda}{2a}\right)^2}}$
D:遅い

で1です。

R.7.7 無線工学B A-8

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R7年7月　無線工学B A-7

平衡二線式給電線と負荷抵抗の間に給電線を挿入するインピーダンス整合に関する問題です。

この問題は全く同じ問題が令和4年7月1回目A-7で出題されています。

下記の記事をご参照ください。

【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 1回目無線工学B A-6~A-10）

１陸技令和4年7月の無線工学B(1回目)の問題を解いてみました。今回はA-6~10です。

答えは

$Z_0$:$\sqrt{RZ_i}$
$l$:$\frac{\lambda}{4}+\frac{n\lambda}{2}$

で2です。

R.7.7 無線工学B A-9

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R7年7月　無線工学B A-7

帯域フィルタ(BPF)を用いた送信アンテナ共用装置に関する問題です。

この問題は全く同じ問題が令和5年7月1回目A-9で出題されています。

下記の記事をご参照ください。

【過去問解説】令和5年7月の1陸技試験問題を解いてみた（R5.7 1回目無線工学B A-6~A-10）

１陸技令和5年7月の無線工学B(1回目)の問題を解いてみました。今回はA-6~10です。

答えは

A:相互
B:結合減衰量
C:奇数倍

で5です。

R.7.7 無線工学B A-10

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R7年7月　無線工学B A-10

円形パラボラアンテナの利得を計算する問題です。

この問題は同様の問題が令和3年7月2回目A-11で出題されています。また、過去に何度も類似問題が出題されています。

解き方については下記の記事をご参照ください。

令和3年7月2回目A-11

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 2回目　無線工学B A-11~A-15）

１陸技令和3年7月の無線工学Bの問題を解いてみました。今回は第2回A-11~15です。

令和4年7月1回目A-13

【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 2回目無線工学B B-1~B-5）

１陸技令和4年7月の無線工B(2回目)の問題を解いてみました。今回はB-1~5です。

令和5年7月1回目A-11

【過去問解説】令和5年7月の1陸技試験問題を解いてみた（R5.7 1回目無線工学B A-11~A-15）

１陸技令和5年7月の無線工学B(1回目)の問題を解いてみました。今回はA-11~15です。

\[ G=\frac{4\pi}{\lambda ^2}A_e \\ =\frac{4\pi}{\lambda ^2}ab\eta_e\eta_h \\ =10\log \left( \frac{4\pi \times 0.14 \times 0.24}{0.05^2}\times 0.77 \times 0.80\right) \\ =10\log (2^2\pi \times 2\times 7 \times 2^3 \times 3\times 3 \times 2^3 \times 10^{-3}) \\ =10(\log \pi +9\log 2 2\log 3 \log 7 -3) \\ =10(2.7+0.5 +2\times 0.48 +0.85 -3) \\ \simeq 20\rm{[dB]} \]

$\log \pi$はA-5で与えられている値を使い、$\log 7$は$\log 6=0.78$以上$\log 8=0.9$以下と考えて$0.85$で計算しています。選択肢の近いものが分かればいいので厳密に計算せず時間を短縮することも重要です。

以上から答えは2です。