令和5年7月の1陸技の試験1回目の無線工学BのA-6~10の問題について解説します。
R.5.7 無線工学B(1回目) A-6

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-6
平行二線式給電線のインピーダンスと等化な静電容量を計算する問題です。
値を変えた同様の問題が令和3年7月1回目A-6で出題されています。 解き方については下記の記事をご参照ください。

平行二線式給電線の特性インピーダンス$Z_0$を計算すると \[ Z_0=276\log_{10}\frac{2D}{d}=276\log_{10}10^2 \\ =552 \] となります。
問題の位置から開放された終端をみたインピーダンス$Z$は \[ Z=\frac{Z_0}{j\tan \left(\frac{2\pi}{\lambda}l\right)} \\ =\frac{z_0}{j\tan \frac{\pi}{3}} \\ =-j\frac{Z_0}{\sqrt{3}} \] となります。
静電容量を$C$とすると \[ Z=\frac{1}{j\omega C} \] なので、 \[ C=\frac{\sqrt{3}}{\omega Z_0} \\ =2.496 \times 10^{-11} \rm{[F]} \\ \simeq 25\rm{[pF]} \] となります。
以上から答えは3です。
終端が短絡されているときは \[ Z=jZ_0\tan \left(\frac{2\pi}{\lambda}l\right) \] となるのでしっかり問題を読んで式を使い分けましょう。
R.5.7 無線工学B(1回目) A-7

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-7
同軸線路の特性インピーダンスに関する問題です。
値を変えた同様の問題が令和3年7月2回目A-6で出題されています。 解き方については下記の記事をご参照ください。

同軸線路の特性インピーダンスは \[ Z_0=\frac{138}{\sqrt{\epsilon_r}}\log \frac{D}{d} \] と表されます。 $\epsilon_r$は誘電体の比誘電率、$D$は外部導体の内径、$d$は内部導体の外径です。
この問題では$d$を$1/2$倍にするとなっているので$D/d$が$8$から$16$になります。 \[ \frac{\log_{10}16}{\log_{10}8}=4/3 \] なので、変更後のインピーダンス$Z’$は \[ Z’=75\times \frac{4}{3}=100\rm{[\Omega]} \] となります。
以上から答えは4です。
R.5.7 無線工学B(1回目) A-8

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-8
電磁波の導体への浸透に関する問題です。
この問題は令和4年1月2回目A-8で同じ問題が出題されています。 この問題とは空欄の位置が異なりますが、同じ問題文が使用されています。
下記の記事をご参照ください。

空欄はそれぞれ
- A:$1/e$
- B:大きく
- C:厚く
が入ります。
答えは3です。
R.5.7 無線工学B(1回目) A-9
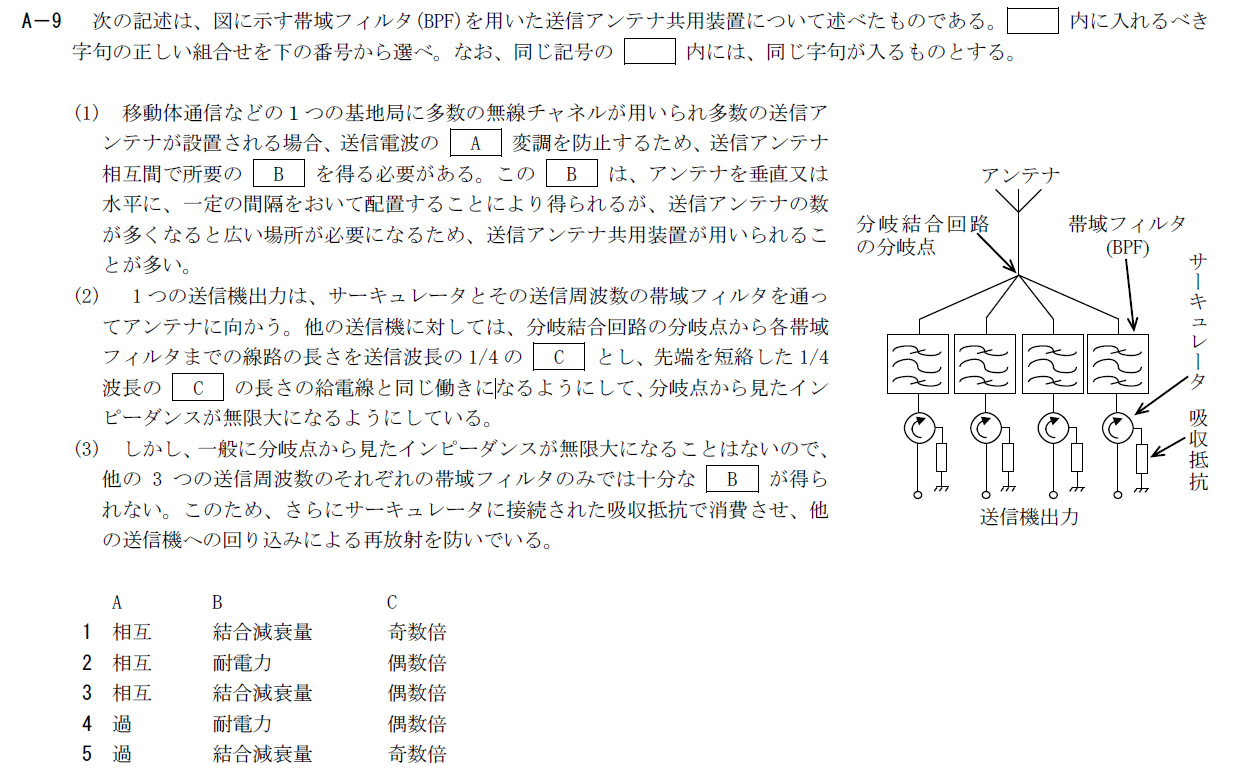
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-9
帯域フィルタ(BPF)を用いた送信アンテナ共用装置に関する問題です。
A
1箇所に複数のアンテナが設置されている場合、互いの送信波により相互変調が発生します。
そのため、Aには「相互」が入ります。
過変調はAMの変調度が100%を越えた時の状態です。
B
Aの相互変調は他の送信機からの強力な入力がある時に発生します。
そのため、送信機相互間に十分なアイソレーションをとる必要があります。
アイソレーションをとるには所要の結合減衰量が必要です。
Bには「結合減衰量」が入ります。
C
分岐点から見たインピーダンスを無限大にするには先端を短絡した1/4波長の奇数倍にすればよいです。
この時、A-6の最後に記載したインピーダンスに$l=1/4\lambda(2n+1)$を代入すると、 \[ Z=jZ_0\tan \left(\frac{2\pi}{\lambda}l\right) \\ =jZ_0 \tan (\pi/2 +n\pi) =\infty \] となります。
そのため、Cには「奇数倍」が入ります。
以上から答えは1です。
R.5.7 無線工学B(1回目) A-10

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月1回目 無線工学B A-10
各種アンテナの特徴に関して誤った選択肢を選ぶ問題です。
この問題は同様の出題形式の問題が複数出ています。 数種類のアンテナのうち5種類が問題文として出題されます。
下記の問題も参考にしてください。
- 令和3年7月2回目A-13
- 令和4年1月1回目A-10
- 令和4年7月1回目A-10
記事のリンクは下記です。



誤った選択肢は3です。
グレゴリアンアンテナの副反射鏡は回転双曲面ではなく、回転楕円面です。
以上から答えは3です。
まとめ
今回は令和5年7月の無線工学B(1回目)の試験A-6~A-10の問題について解説しました。 特にA-10のような問題は毎年のように出題されています。 複数のアンテナに関する理解する必要がありますが、それぞれざっくり知っていれば解ける問題です。 落ち着いて消去法で解くのがよいでしょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント