【過去問解説】令和6年1月の1陸技試験問題を解いてみた（R6.1 無線工学A A-6~A-10）

令和6年1月の1陸技の無線工学AのA-6～10の問題について解説します。

R.6.1 無線工学A A-6
R.6.1 無線工学A A-7
R.6.1 無線工学A A-8
R.6.1 無線工学A A-9
R.6.1 無線工学A A-10
1. A
2. B
3. C
4. D
まとめ
参考文献

R.6.1 無線工学A A-6

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年1月　無線工学A A-6

振幅変調の二乗検波に関する計算問題です。

この問題は同様の問題が令和4年7月2回目A-5で出題されています。計算するものが違うのと、信号を令和4年7月2回目A-5では $\sin$ で表しているのに対して、この問題では $\cos$ で表しています。

計算方法はほとんど同じなのでこちらの記事をご参照ください

【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 2回目無線工学A A-1~A-5）

１陸技令和4年7月の無線工A(2回目)の問題を解いてみました。今回はA-1~5です。

計算結果は下記のとおりです。 $(信号波成分)=\frac{kA^2}{2}\left(1+\frac{m^2}{2}\right)+kA^2m\cos pt +\frac{kA^2m^2}{4}\cos 2pt$ 第一項は直流成分、第二項は信号波成分、第三項は信号波の第二高調波成分です。

求めるのは信号波成分と信号波の第二高調波成分の実効値なので、 $E=\sqrt{\left(\frac{kA^2m}{\sqrt{2}}\right)^2+\left(\frac{kA^2m^2}{4\sqrt{2}}\right)^2}=\frac{kA^2m}{\sqrt{2}}\sqrt{1+\left(\frac{m}{4}\right)^2}$ となります。

以上から答えは4です。

R.6.1 無線工学A A-7

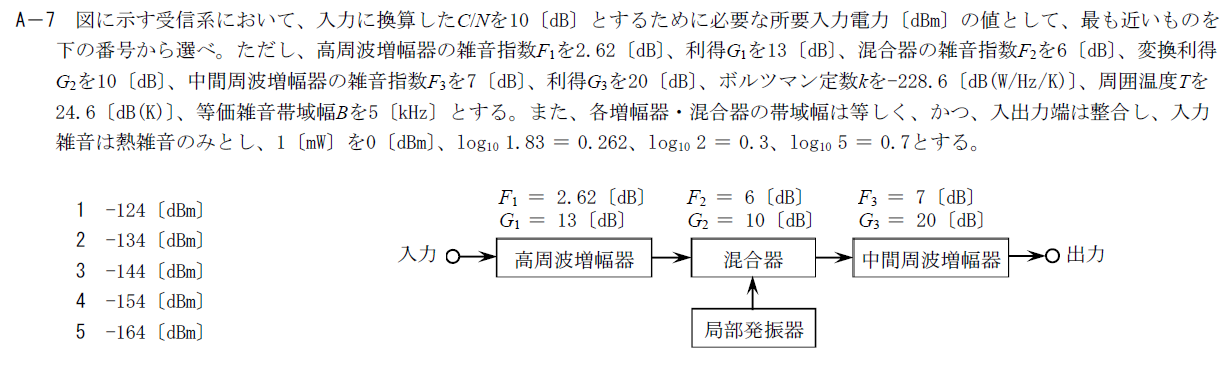
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年1月　無線工学A A-7

受信機の雑音に関する問題です。

類似問題が令和3年7月1回目A-8や令和4年1月1回目A-8で出題されています。この問題に限った話ではありませんが、雑音指数を真数で計算したうえでデシベルで計算結果を求めるというかなり面倒くさい問題となっています。

下記の記事も参考にしてください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学A A-6~A-10）

１陸技令和4年1月の無線工学A(1回目)の問題を解いてみました。今回はA-6~10です。

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 1回目　無線工学A A-6~A-10）

１陸技令和3年7月の無線工学Aの問題を解いてみました。今回は第1回A-6~10を解きました。

まず全体の雑音指数を求めるために各パラメータを真数に直します。

項目	デシベル	真数
$F_1$	2.62	1.83
$F_2$	6	4
$F_3$	7	5
$G_1$	13	20
$G_2$	10	10
$G_3$	20	100

全体の雑音指数 $F$ は $F=F_1+\frac{F_2-1}{G_1}+\frac{F_3-1}{G_1G_2}　\\ =1.83+0.15+0.02 \\ =2(真数) =3\rm{[dB]}$

受信機の入力換算の雑音 $N$ は $N=FkTB$ （真数）で表せます。

そのため、 $N=3-228.6+24.6+37 \\ =-164\rm{[dBW]} \\ =-134\rm{[dBm]} \\$ となります。

入力電力を $P_I$ とすると、入力換算の $C/N$ は $10\rm{[dB]}$ なので $P_I-N=10 \\ P_I=-124\rm{[dBm]}$

以上から答えは1です。

R.6.1 無線工学A A-8

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年1月　無線工学A A-8

無停電電源装置(UPS)に関して誤った選択肢を選ぶ問題です。

この問題は同様の問題が令和4年7月1回目A-10で出題されています。

下記の記事もご参照ください。

【過去問解説】令和4年7月の1陸技試験問題を解いてみた（R4.7 1回目無線工学A A-6~A-10）

１陸技令和4年7月の無線工学A(1回目)の問題を解いてみました。今回はA-6~10です。

誤った選択肢は5です。

一括バイパス方式並列冗長システムでは容量や設計・技術等が異なるUPSを混在させるのは技術的に難しいです。

そのため、答えは5です。

R.6.1 無線工学A A-9

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年1月　無線工学A A-9

単結晶シリコン太陽電池に関する問題です。

この問題は同様の問題が令和3年7月1回目A-10で出題されています。

下記の記事もご参照ください。

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 1回目　無線工学A A-6~A-10）

１陸技令和3年7月の無線工学Aの問題を解いてみました。今回は第1回A-6~10を解きました。

誤った選択肢は3です。

変換効率に関する内容で真性変換効率と実効変換効率の関係が逆です。

真性変換効率は面積として電極等を除いた光電効果のある面積を用いた変換効率です。

一方、実効変換効率は太陽電池の全面積を用います。全面積の方が実際に使う太陽電池の面積となるので実効的な値となるためこのような呼び名になっています。

以上から答えは3です。

R.6.1 無線工学A A-10

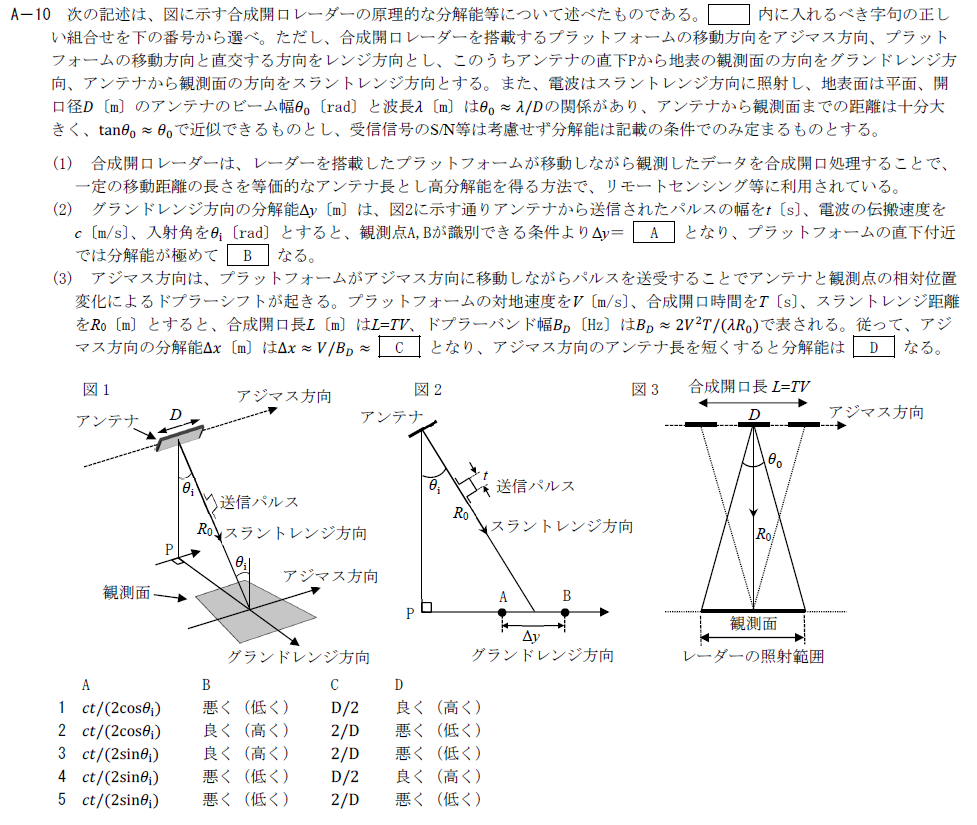
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R6年1月　無線工学A A-10

合成開口レーダーの原理的な分解能に関する問題です。

あまり出題されておらず新傾向の問題と思って差し支えないでしょう。

A

観測点A及びBで反射した電波がアンテナに戻るまでの時間をそれぞれ $T_A,T_B$ とすると $T_A=(2R_0-\Delta y\sin \theta _i)/c \\ T_B=(2R_0+\Delta y\sin \theta _i)/c$ となります。

この2点間の時間差 $T_d$ は $T_d=(2\Delta y\sin theta_i)/c$ となります。

パルス幅 $t$ がこの時間差以下の時は2つの観測点を区別できなくなります。

そのため $\Delta y=ct/(2\sin \theta_i)$ となり、Aには「 $ct/(2\sin \theta_i)$ 」が入ります。

B

プラットフォーム直下付近では $\theta_i$ が $0$ 付近になるため、分母が非常に小さくなり $\Delta y$ が非常に大きくなります。

そのため、Bには「悪く（低く）」が入ります。

C

問題文から $\Delta x \simeq V/B_D = \frac{V\lambda R_0}{2V^2T} \\ =\frac{\lambda R_0}{2VT}=\frac{\lambda R_0}{2L}$ ここで $\lambda =\theta_0 D$ なので $\Delta x=\frac{\theta_0 DR_0}{2L}$ 図3から $\theta_0R_0 \simeq L$ なので $\Delta x\simeq D/2$ となり、Cには「 $D/2$ 」が入ります。