令和6年1月の1陸技の無線工学AのA-11~15の問題について解説します。
R.6.1 無線工学A A-11

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年1月 無線工学A A-11
GPSの誤差補正に関する問題です。
この問題は同様の問題が令和3年7月2回目A-11で出題されています。
下記の記事をご参照ください

誤った選択肢は2です。
対流圏遅延量は周波数に依存しないため、2周波以上を測定をしても誤差の補正はできません。
そのため答えは2です。
R.6.1 無線工学A A-12

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年1月 無線工学A A-12
デジタル無線方式のフェージング補償技術に関して誤った選択肢を選ぶ問題です
類似問題が令和3年7月1回目A-17や令和5年1月1回目A-13で出題されています。
下記の記事もご参照ください。


誤った選択肢は1です。
BCH符号はバースト誤りではなくランダム誤りに強い誤り訂正符号です。バースト誤りの誤り訂正にはリード―ソロモン符号などが強いです。
そのため答えは1です。
R.6.1 無線工学A A-13

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年1月 無線工学A A-13
相互変調積に関する問題です。
この問題は同様の問題が令和3年7月1回目B-4や令和4年1月1回目A-3で出題されています。
下記の記事もご参照ください。


相互変調積は三角関数の積の計算が大量に出てくるので計算が非常に大変です。 受信機に大きな影響を与えるのは基本的には3次の相互変調積なので、試験で出題されやすいのもその付近です。 具体的には$2f_1\pm f_2$や$2f_2\pm f_1$の項となります。$\omega_1=2\pi f_1, \omega_2=2\pi f_2$です。
$\sin$の形で書かれた2波の計算は令和3年7月1回目B-4で計算しています。 ここでは今一度3次の高調波を計算して、計算しなくても係数がどうなるか解説します。
3次の高調波なので下記の項に含まれます。 \[ e_i^3=A_1^3\sin^3(\omega_1 t)+3A_1^2A_2\sin^2(\omega_1 t)\sin(\omega_2 t)+3A_1A_2^2\sin(\omega_1 t)\sin^2(\omega_2 t)+A_2^3\sin^3(\omega_2 t) \] $2f_1\pm f_2$や$2f_2\pm f_1$の周波数を持つ項は第2項と第3項です。 \[ (第2項)=3A_1^2A_2\frac{1}{2}(1-\cos(2\omega_1t))\sin\omega_2t \\ =\frac{3}{2}A_1^2A_2\sin\omega_2 t-\frac{3}{4}A_1^2A_2(\cos(2\omega_1+\omega_2)t+\sin(2\omega_1-\omega_2)t) \\ =\frac{3}{2}A_1^2A_2\sin\omega_2 t-\frac{3}{4}A_1^2A_2\cos(2\omega_1+\omega_2)t-\frac{3}{4}A_1^2A_2\sin(2\omega_1-\omega_2)t \] \[ (第3項)=3A_1^2A_2\frac{1}{2}(1-\cos(2\omega_2t))\sin\omega_1t \\ =\frac{3}{2}A_1^2A_2\sin\omega_1 t-\frac{3}{4}A_1^2A_2(\cos(2\omega_2+\omega_1)t+\sin(2\omega_2-\omega_1)t) \\ =\frac{3}{2}A_1^2A_2\sin\omega_1 t-\frac{3}{4}A_1^2A_2\cos(2\omega_2+\omega_1)t-\frac{3}{4}A_1^2A_2\sin(2\omega_2-\omega_1)t \]
問題となる3次の相互変調積の係数としては必ず$3/4$がかかり、三角関数の中の周波数で2倍になっている信号の振幅の二乗ともう一方の信号の振幅がかかっています。
この決まりをもとに問題文を見ると$2\omega_2-\omega_1$の係数は \[ 3a_3AB^2/4 \] となるはずです。
そのため、答えは2です。
R.6.1 無線工学A A-14

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年1月 無線工学A A-14
衛星通信回線の割当方式に関する問題です。
この問題は全く同じ問題が令和4年1月1回目A-14で出題されています。
下記の記事をご参照ください。

- A:プリアサイメント
- B:少ない
- C:デマンドアサイメント
- D:小さな
が入り、答えは1です。
R.6.1 無線工学A A-15
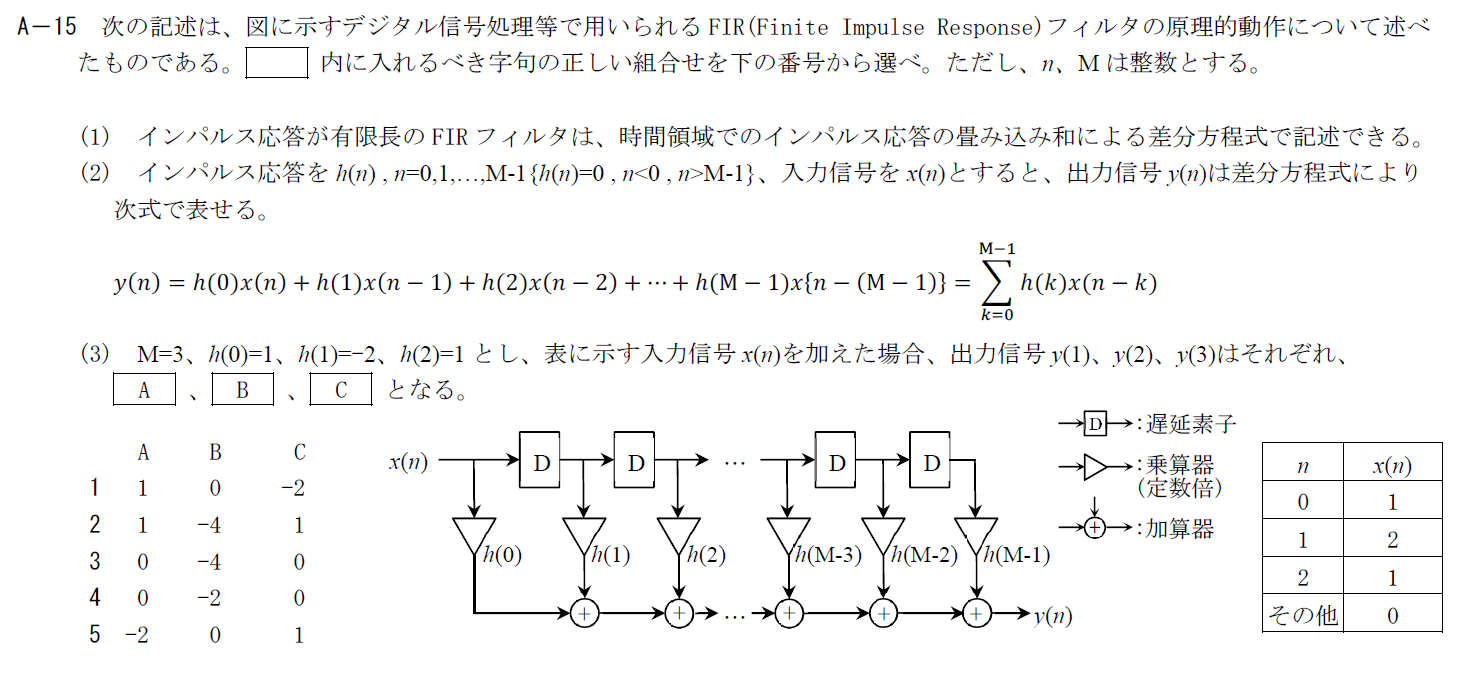
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年1月 無線工学A A-15
FIRの原理的動作に関する計算問題です。
この問題は同様の問題が令和4年1月2回目A-15で出題されています。
下記の記事もご参照ください。

計算方法は全く同じで
\[ y(n)=\sum^{M-1}_{k=0}h(k)x(n-k) \] を使って \[ y(1)=h(0)x(1)+h(1)x(0)=2-2=0 \\ y(2)=h(0)x(2)+h(1)x(1)+h(2)x(0)=1-4+1=-2 \\ y(3)=h(1)x(2)+h(2)x(1)=-2+2=0 \]
以上から答えは4です。
まとめ
今回は令和6年1月の無線工学Aの試験A-11~A-15の問題について解説しました。 今回の問題は過去問類似問題が多かったです。 計算問題も多いのでうっかりミスに注意しましょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント