令和6年1月の一陸技の試験の無線工学BのA-11~15の問題について解説します。
R.6.7 無線工学B A-11

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-11
グレゴリアンアンテナに関する問題です。
この問題は同様の問題が令和4年7月1回目A-12で出題されています。 問題文は同じで、空欄の位置が違います。
下記の記事もご参照ください。

A,B
グレゴリアンアンテナは図のような構造になっています。 副反射鏡は回転楕円面の形状をしています。

グレゴリアンアンテナの概要
副反射鏡として回転楕円面の凹面を使うことにより開口面で電波の位相をそろえることができます。
そのため、Aには「回転楕円面」、Bには「凹面側」が入ります。
C
グレゴリアンアンテナではパラボラアンテナと同様に主反射鏡の焦点にある副反射鏡によるブロッキングが起きます。
そのため、Cには「副反射鏡」が入ります。
以上から答えは5です。
R.6.7 無線工学B A-12

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-12
誘電体レンズアンテナに関して誤った選択肢を選ぶ問題です。
この問題は同様の問題が令和4年1月2回目A-10で出題されています。 下記の記事をご参照ください。

誘電体レンズアンテナの原理に関しては下記で解説していますのでご参照ください。 令和3年7月1回目A-10、令和4年7月1回目A-11、令和5年7月2回目A-13で出題されています。
令和3年7月1回目A-10

誤った選択肢は3です。
原理の問題に描かれた図からも分かるように屈折率が1より大きい時の誘電体レンズの形状は凸レンズとなります。
そのため答えは3です。
R.6.7 無線工学B A-13
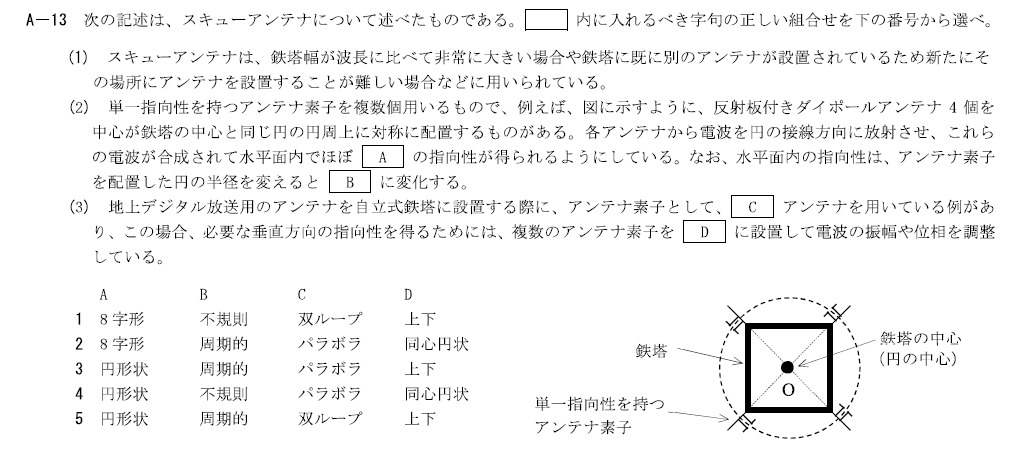
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-13
スキューアンテナに関する問題です。 これまでスキューアンテナについて出題されたことはあまりないので新傾向と思ってよいでしょう。
スキューアンテナは鉄塔に対して斜向してアンテナを配列することで既存のアンテナや鉄塔に大きな影響を与えることなく新たなアンテナを設置する手法です。
詳細は問題を見ながら見ていきましょう。
A
アンテナを鉄塔の中心を中心とした円周上に対称にアンテナを配置します。
合成パターンの落ち込みを最小にするように配置を調整することで水平面内にはほぼ円形状の指向性を得ることができます。
そのため、Aには「円形状」が入ります。
B
配置する円の半径を変化させることで波長に合わせて周期的に指向性が変化します。
そのため、Bには「周期的」が入ります。
C
アンテナとしては双ループアンテナなどが使用されています。 例えば、東京スカイツリーでは4L双ループアンテナが使用されています。 パラボラアンテナでは指向性が強すぎるので円形状の指向性は難しいでしょう。
そのためCには「双ループ」が入ります。
D
Cに引き続き東京スカイツリーの例に関する内容と思われます。
東京スカイツリーでは1系統当たり、4段×20面のアンテナが配置されています。 この4段は上下方向に配置され、位相や振幅を調整して放射することで都市部方向に強い電界強度を得るようなチルトを実現しています。
そのため、Dには「上下」が入ります。
東京スカイツリーのアンテナに関しては下記のサイトで詳しく説明されています。

R.6.7 無線工学B A-14

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-14
SHFやEHFの降雨時に生じる交差偏波に関して誤った選択肢を選ぶ問題です。
この問題は全く同様の問題が令和3年7月1回目A-15で出題されています。
下記の記事もご参照ください。

誤った選択肢は2です。
交差偏波識別度の定義は \[ 20\log_{10}(E_p/E_c) \] となります。
分母と分子が逆です。
以上から答えは2です。
R.6.7 無線工学B A-15

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R6年7月 無線工学B A-15
送信アンテナと受信アンテナの高さを固定して距離を近づけた時に、受信電界強度がゼロになる距離を求める問題です。
考え方としてはいわゆる2波モデルで考えることができます。
2波モデルについては下記の記事で令和4年1月1回目A-14をご参照ください。

問題としては2波モデルにおいて下記で表される電界強度がゼロになるような距離を求めることになります。 \[ E=E_0|\sin (\phi /2)| \]
ここでは$\sin (\phi /2)=0$となるような距離を求めます。
位相差$\phi$は \[ \phi=\frac{4\pi h_t h_r}{\lambda d} \] なので、 \[ \frac{4\pi h_t h_r}{2\lambda d}=n\pi \] となればよいと言えます。 ここで$h_t,h_r$はそれぞれ送信アンテナと受信アンテナの高さ、$d$はアンテナ間の距離、$n$は整数です。
$h_t=100, h_r=20, \lambda =1$なので \[ \frac{4000}{d}=n \] となります。
最初は$d=5000$なので、$d$を小さくすることで$4/5$より大きい最小の整数になるような$d$を考えます。
この条件を満たす整数$n$は$1$なので$d=4000$が最初に電界強度がゼロとなります。
以上から答えは4です。
まとめ
今回は令和6年7月の無線工学Bの試験A-11~A-15の問題について解説しました。 スキューアンテナのような見慣れない問題もあり、戸惑うこともあるかもしれません。 落ち着いて問題文の誘導に従えば、想定されている例を知らなくても解くことは可能でしょう。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント