令和4年7月の1陸技の試験、無線工学AのA-11~15の問題について解説します。
R.4.7 無線工学A(2回目) A-11

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-11
航空用無線施設に関して誤った選択肢を選ぶ問題です。
誤った選択肢は4です。
誤っているのはグライド・パスに関して記載されている記述で、ここにはVHF帯の電波を使用すると記載されています。
グライド・パスはVHF帯ではなく、UHF帯の電波を使用します。
そのため、答えは4です。
R.4.7 無線工学A(2回目) A-12

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-12
レーダー方程式を使ってパルスレーダーの最大探知距離を計算する問題です。
令和3年7月1回目のA-12で値違いの類似の問題が出ています。 計算式はこの問題と同じで、値を代入するだけです。

計算式の導出は令和4年1月1回目A-12を参考にしてください。

\[ R=\sqrt[4]{\frac{PG\sigma A_e}{(4\pi)^2S}} \]
問題文の値を代入すると \[ R=\sqrt[4]{10^{16}}=10^4\rm{[m]} \] となります。
以上から答えは1です。
R.4.7 無線工学A(2回目) A-13

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-13
この問題は令和4年1月2回目のB-1の問題で同じ問題が出ています。 こちらの問題の方が範囲が広いため下記をご参照ください。

答えは5です。
R.4.7 無線工学A(2回目) A-14

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-14
BPSK信号を同期検波したときに発生するビット誤り率に関する問題です。
ほぼ同じ問題が令和3年7月1回目のA-13で出題されています。

BとCについては上記の問題とは逆で$CNR$について聞かれていることには注意しましょう。
B
$CNR$は搬送波電力と雑音電力の比なので \[ CNR=\frac{A^2}{2\sigma^2} \] となります。
これを$\sqrt{A^2/(2\sigma^2)}$に代入すると$\sqrt{CNR}$となります。
そのため、Bには「$\sqrt{CNR}$」が入ります。
C
上記の記事の通り、$CNR$の方が$SNR$より3[dB]低くなります。
そのため、Cには「低い」が入ります。
以上から答えは2です。
R.4.7 無線工学A(2回目) A-15
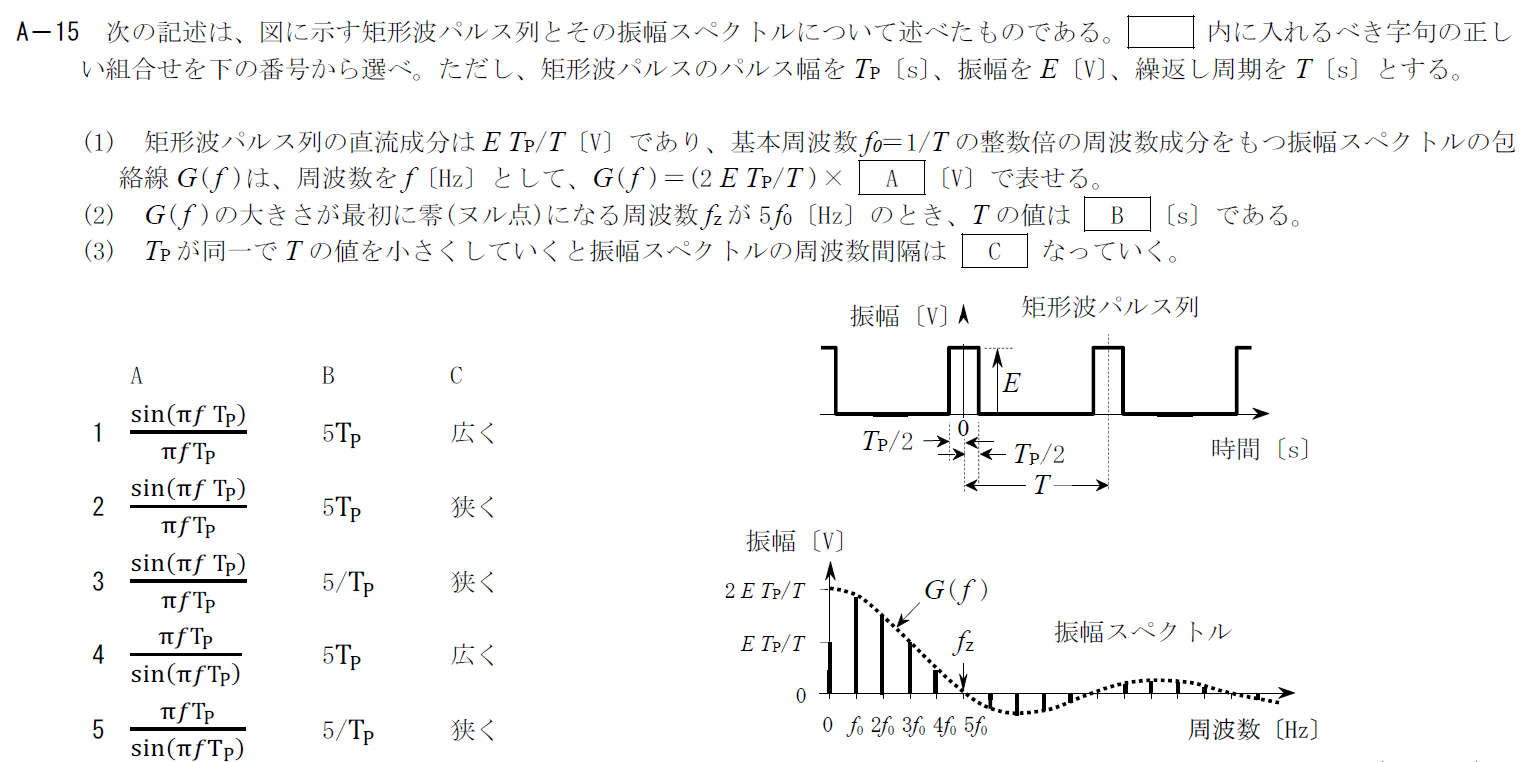
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R4年7月2回目 無線工学A A-15
矩形波パルスとそのフーリエ級数展開に関する問題です。
A
パルス波形を$P(t)$とすると次のように表されます。 \[ P(t)=\left\{ \begin{array}{l} E \qquad (n+1)T-T_P/2 \leq t \leq (n+1)T+T_P/2 \\ 0 \qquad nT-T_P/2 \leq t \leq nT+T_P/2 \end{array} \right. \] $n$は整数です。
フーリエ級数展開は次のようになります。 \[ P(t)=\sum^{\infty}_{n=-\infty}C_n e^{j\omega_0 nt} \] ここで$\omega_0=2\pi f_0=\frac{2\pi}{T}$です。
$C_n$を計算すると次のようになります。 \[ C_n=\frac{1}{T}\int^{T+T_P/2}_{T_P/2}P(t)e^{-j\omega_0 nt}dt \\ =\frac{1}{T}\int^{T+T_P/2}_{T-T_P/2}Ee^{-j\omega_0 nt}dt \\ \] $n=0$の時 \[ C_n=\frac{E}{T}(T+\frac{T_P}{2}-T+\frac{T_P}{2})=\frac{T_P}{T}E \\ \] $n\neq 0$の時 \[ C_n=\frac{E}{T}\left[\frac{1}{-j\omega_0 n} e^{-j\omega_0 nt}\right] =\frac{E}{T}\frac{T}{2\pi n}je^{-j2\pi n}(-1)2j\sin \frac{T_P}{T}n\pi \\ =\frac{E}{n\pi}\sin \left(\frac{T_P}{T}n\pi \right)\\ =\frac{ET_P}{T}\frac{\sin (\pi f T_P)}{\pi f T_P} \] ここで$f=nf_0$です。
係数の2が合いませんが、何度か検算し、$n=0$のみ不連続となるのは不自然なため、こちらの計算が正しいと思われます。
ここではパルス波をフーリエ級数展開すると$\frac{\sin \omega t}{\omega}$の形になることを押さえておきましょう。
上記からAには「$\frac{\sin (\pi f T_P)}{\pi f T_P}$」が入ります。
B
最初のヌル点は分子が最初にゼロとなる点です。 つまり$f=f_Z$の時は \[ \pi f_Z T_P=\pi \] です。 $T$について解くと \[ T=5T_P \] となります。
そのため、Bには「$5T_P$」が入ります。
C
振幅スペクトルはは$f_0$間隔で現れるので、$T$を小さくすると$f_0$が大きくなります。 つまり、周波数間隔が広くなるということです。
そのため、Cには「広く」が入ります。
以上から答えは1です。
まとめ
少し間が空きましたが令和4年7月の2回目の無線工学A A-11~15の問題を解説しました。 フーリエ変換の考え方が必要な問題も出題されています。 計算自体はできなくても大丈夫ですが、試験以外でもよく使うので身に着けておくといいでしょう。 年内には7月分の無線工学AとBの解説をすべて完了したいと思います。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント