令和5年7月の1陸技の試験2回目の無線工学AのB-1~5の問題について解説します。
R.5.7 無線工学A(2回目) B-1

出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月2回目 無線工学A B-1
地上マイクロ波多重回線の中継方式に関する問題です。
類似問題が令和4年1月1回目A-13で出題されています。 文章の内容はかなり異なるので1つずつ見ていきましょう
下記の記事もご参照ください。

ア、イ
オーバーリーチ干渉は同じ周波数の中継局同士が干渉して通信品質が劣化する現象です。
このオーバーリーチ干渉を軽減するためには同一の周波数の中継局同士が中継ルート上で直接つながらないようにすればよいです。
これを実現するためには中継ルートをジグザグにして、各中継局から電波が直線的に届くようにアンテナの指向性を利用すればよいということになります。
そのため、アには1.「ジグザグ」、イには3.「指向性」が入ります。
ウ
(2)の説明では、中継局は周波数を変換し増幅するだけで、変復調回路を持たない(復調しない)ので信号波再生されていません。
この動作はヘテロダイン受信機と同じです。
そのため、ウには7.「非再生(ヘテロダイン)」が入ります。
エ
再生中継方式では元の信号のパルス列で再度変調します。 デジタル変調であれば、ビット列が変化しない限り変調しなおせば波形がひずむことがありません。
そのため、エには4.「されない」が入ります。
オ
(4)の方式は周波数を変換したり、電力を増幅したりしないので無給電中継方式と呼ばれています。
そのため、オには10.「無給電」が入ります。
R.5.7 無線工学A(2回目) B-2
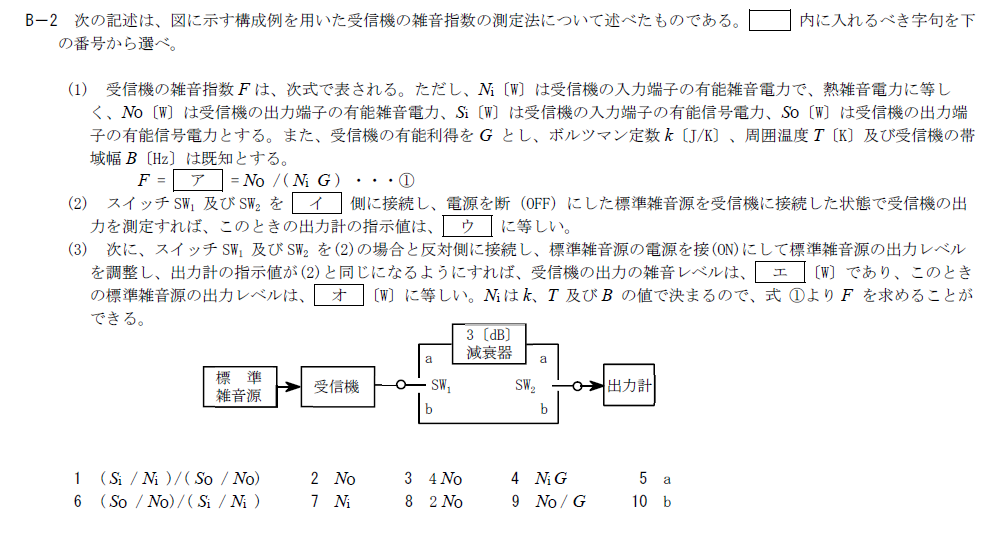
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月2回目 無線工学A B-2
受信機の雑音指数の測定に関する問題です。
全く同じ問題が令和4年1月1回目B-3で出題されています。
下記の記事をご参照ください。

答えは下記のとおりです。
- ア:1.「$(S_i/N_i)/(S_O/N_O)$」
- イ:10.「b」
- ウ:2.「$N_O$」
- エ:8.「$2N_O$」
- オ:9.「$N_O/G$」
R.5.7 無線工学A(2回目) B-3
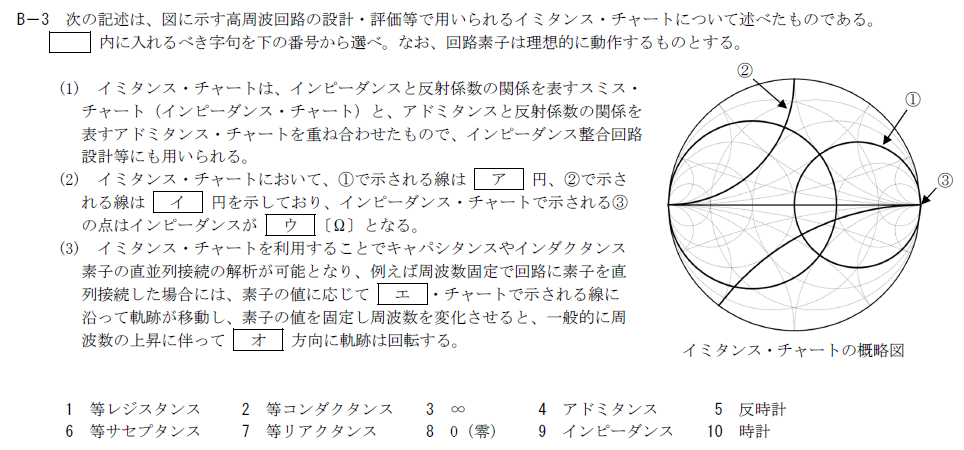
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月2回目 無線工学A B-3
イミタンス・チャートに関する問題です。
イミタンス・チャートに関する問題は令和5年1月2回目A-16で出題されています。
下記の記事もご参照ください。

ア
ここは用語に関する空欄です。 ①は等レジスタンス円で純抵抗が同じ点の集まりです。
そのため、アには1.「等レジスタンス」が入ります。
イ
②は等サセプタンス円です。
イには6.「等サセプタンス」が入ります。
ウ
③の点はインピーダンスが$0\rm{[\Omega]}$を表すのでウには8.「0(零)」が入ります。
エ
素子を直列に接続した場合、インピーダンスチャート上の線に沿って移動します。
そのため、エには9.「インピーダンス」が入ります。
オ
素子を一定にして周波数を変化させた場合、純抵抗は変化しないので等レジスタンス円上を移動します。
インピーダンスの虚部は \[ \omega L-\frac{1}{\omega C} \] で表されます。
周波数を上昇させると誘導性の$\omega L$が大きくなり、容量性の$\frac{1}{\omega C}$が小さくなるので、周波数の上昇は誘導性の素子を直列に接続したことを意味します。
誘導性の成分を直列に接続すると等レジスタンス円を時計回りに移動します。
そのため、オには10.「時計」が入ります。
R.5.7 無線工学A(2回目) B-4
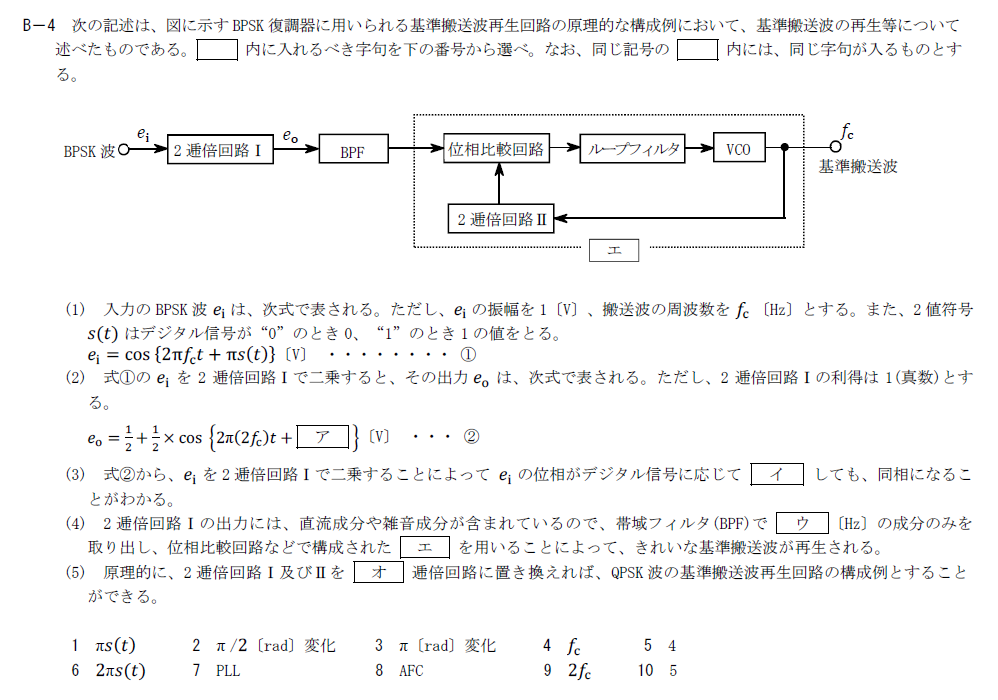
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月2回目 無線工学A B-4
BPSK復調器の基準搬送波再生回路に関する問題です。
この問題は全く同じ問題が令和4年7月1回目B-1で出題されています。
下記の記事をご参照ください。

答えは
- ア:6.「$2\pi s(t)$」
- イ:3「$\pi\rm{[rad]}$変化」
- ウ:9.「$2f_C$」
- エ:7.「PLL」
- オ:5.「4」
です。
R.5.7 無線工学A(2回目) B-5
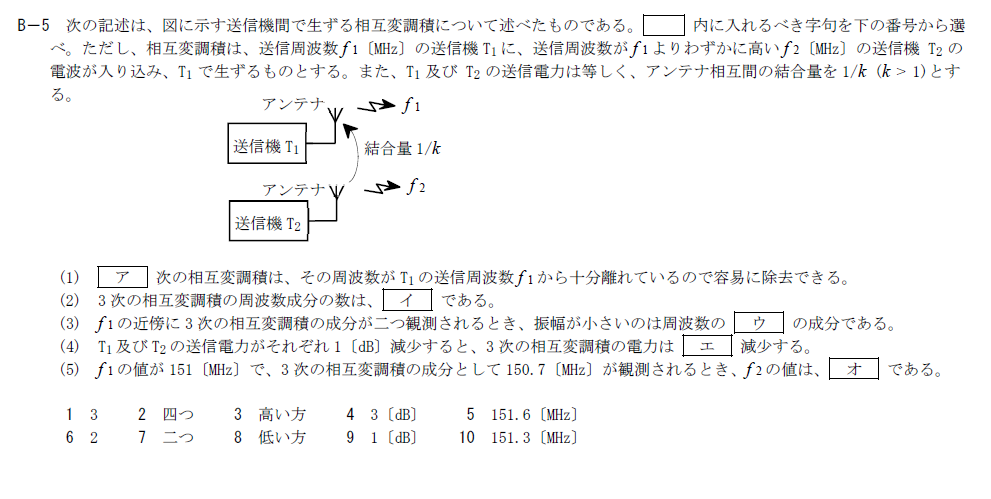
出典:公益財団法人 日本無線協会 第一級陸上無線技術士 R5年7月2回目 無線工学A B-5
相互変調積に関する問題です。
相互変調積に関する問題は過去問でも何度か出題されています。 例えば令和4年7月2回目A-8や令和3年7月1回目B-4などです。
下記の記事もご参照ください。
令和4年7月2回目A-8

令和3年7月1回目B-4

ア
2次の相互変調積は$f_2-f_1$と$f_+f_2$の2種類ですが、いずれも$f_1$から十分離れています。
そのため、アには6.「2」が入ります。
イ
3次の相互変調積は$2f_1-f_2, 2f_2-f_1,2f_1+f_2,2f_2+f_1$の4種類です。
そのため、イには2.「四つ」が入ります。
ウ
$f_1$に近い成分は$2f_1-f_2$と$2f_2-f_1$の2つです。 振幅が小さいのはアンテナ相互間の結合量が$1/k$になる分$f_2$の成分が小さくなります。
振幅については令和3年7月1回目B-4をご参照ください
そのため、振幅が小さい成分は$2f_2-f_1$です。 $f_2$の方が周波数が高いので$2f_2-f_1$は高い成分でウには3.「高い方」が入ります。
エ
3次の相互変調積は振幅の3乗に比例するのでそれぞれ$1\rm{[dB]}$減衰すると全部で$3\rm{[dB]}$減衰します
そのため、エには4.「$3\rm{[dB]}$」が入ります。
オ
問題文から$f_2>f_1$なので、$f_1$より低い相互変調積になるのは$2f_1-f_2$の成分です。
計算すると \[ 2f_1-f_2=150.7 \\ f_2=2f_1-150.7 =2\times 151-150.7=151.3 \rm{[MHz]} \] で、オには10.「$151.3 \rm{[MHz]}$」が入ります。
まとめ
今回は令和5年7月の無線工学A(1回目)の試験B-1~B-5の問題について解説しました。 いつもなら正誤問題が1,2問入っていますが、今回はすべて穴埋め問題でした。 最初の空欄を間違えると全ての答えがずれる問題がありますので、注意して問題に取り組みましょう。
今回で令和5年7月分の試験の解説が終了しました。また来年の1月の試験から過去問解説を実施します。それまでは一旦不定期更新です。
参考文献
電磁気学をちゃんと学びたい人向け
上の難易度が高い人



コメント