【過去問解説】令和5年7月の1陸技試験問題を解いてみた（R5.7 2回目 無線工学B A-16~A-20）

令和5年7月の1陸技の試験2回目の無線工学BのA-16～20の問題について解説します。

R.5.7 無線工学B（2回目） A-16

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学B A-16

等価地球上にあるアンテナからの電波の見通し距離に関する問題です。

この問題は全く同じ問題が令和3年1月1回目A-14で出題されています。
また、同様の式を使った計算問題が令和4年1月2回目A-17でも出題されています。

下記の記事をご参照ください。

【無線】1月の1陸技試験問題を解いてみた（R3.1 1回目　無線工学B A-11~A-15）

１陸技令和3年の無線工学Bの問題を解いてみました。今回は第2回A-11~15を解きました。

jr2kcb.com

2021.03.14

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 2回目 無線工学B A-16~A-20）

１陸技令和4年1月の無線工学B(2回目)の問題を解いてみました。今回はA-16~20です。

jr2kcb.com

2022.04.30

空欄は

• A:$\cos \theta$
• B:$\frac{d}{KR}$
• C:$\sqrt{2kRh}$

で答えは4です。

R.5.7 無線工学B（2回目） A-17

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学B A-17

対流圏伝搬におけるフェージングの主に用語の意味を問う問題です。

この問題はほぼ同じ問題が令和4年1月2回目A-16で出題されています。
Cの空欄の部分が「大きくなる」と「小さくなる」で異なることには注意しましょう。

こちらの記事をご参照ください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 2回目 無線工学B A-16~A-20）

１陸技令和4年1月の無線工学B(2回目)の問題を解いてみました。今回はA-16~20です。

jr2kcb.com

2022.04.30

空欄は

• A:大気の屈折率
• B:大地反射波
• C:大きく

で答えは4です。

R.5.7 無線工学B（2回目） A-18

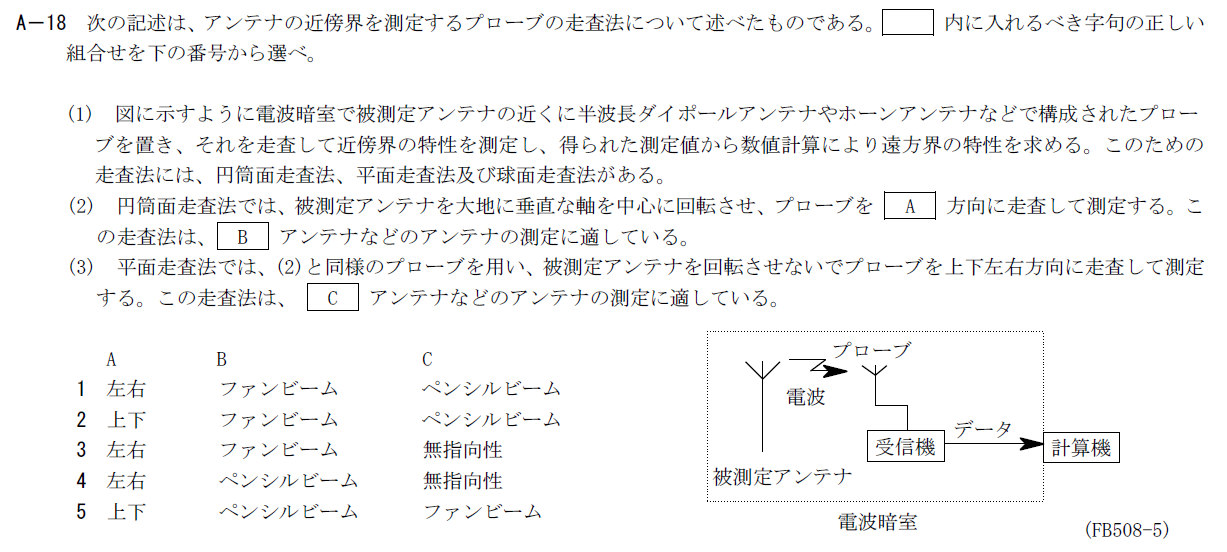
出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学B A-18

アンテナの測定方法に関する問題です。

この問題はほぼ同じ問題が令和3年7月1回目A-18で出題されています。

文章の内容的には(2)が令和3年7月1回目A-18の(2)、(3)が令和3年7月1回目A-18の(1)と同じです。

空欄の位置を気にしなければそれぞれ同じ文章になっています。

下記の記事をご参照ください。

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 1回目　無線工学B A-16~A-20）

１陸技令和3年7月の無線工学Bの問題を解いてみました。今回は第1回A-16~20を解きました。

jr2kcb.com

2021.08.21

空欄は

• A:上下
• B:ファンビーム
• C:ペンシルビーム

で答えは2です。

R.5.7 無線工学B（2回目） A-19

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学B A-19

無損失給電線の終端を短絡した時と開放した時それぞれのインピーダンスが分かっているときの無損失給電線の特性インピーダンスを計算する問題です。

特性インピーダンスを$Z_0$とすると開放時のインピーダンス$Z_O$と短絡時のインピーダンス$Z_S$はそれぞれ
$$Z_O=-j\frac{Z_0}{\tan \beta l} \\ Z_S=jZ_0\tan \beta l$$
となります。

与えられたインピーダンスの値を代入して計算すると
$$\tan \beta l=\frac{Z_0}{120}\\ Z_0^2=120 \times 30 =60^2 \\ Z_0=60\rm{[\Omega]}$$
となります。

以上から答えは4です。

同様に終端を開放したり短絡した時のインピーダンスの式を使う問題は過去にも出題されています。

例えば下記の問題があります。

令和5年7月1回目A-6(開放時)

【過去問解説】令和5年7月の1陸技試験問題を解いてみた（R5.7 1回目 無線工学B A-6~A-10）

１陸技令和5年7月の無線工学B(1回目)の問題を解いてみました。今回はA-6~10です。

jr2kcb.com

2023.07.22

令和3年7月2回目A-8(短絡時)

【過去問解説】令和3年7月の1陸技試験問題を解いてみた（R3.7 2回目　無線工学B A-6~A-10）

１陸技令和3年7月の無線工学Bの問題を解いてみました。今回は第2回A-6~10です。

jr2kcb.com

2021.10.17

R.5.7 無線工学B（2回目） A-20

出典：公益財団法人　日本無線協会　第一級陸上無線技術士　R5年7月2回目　無線工学B A-20

Y係数法を使った雑音温度の測定法に関する問題です。

全く同じ問題が令和4年1月1回目A-18で出題されています。

下記の記事をご参照ください。

【過去問解説】令和4年1月の1陸技試験問題を解いてみた（R4.1 無線工学B A-16~A-20）

１陸技令和4年1月の無線工学B(1回目)の問題を解いてみました。今回はA-16~20です。

jr2kcb.com

2022.02.19

空欄は

• A:$\frac{T_0+T_R}{T_N+T_R}$
• B:$\frac{T_0-Y_1T_N}{Y-1}$
• C:$\frac{T_N+T_R}{Y_1}-T_R$

で答えは5です。

まとめ

今回は令和5年7月の無線工学B(2回目)の試験A-16~A-20の問題について解説しました。
少し応用する問題や過去問から少し内容を変更した問題が出題されていました。
過去問の丸暗記では解けないので気を付けましょう。

勉強法

第一級陸上無線技術士の勉強法とおすすめ参考書

参考文献

電磁気学をちゃんと学びたい人向け

上の難易度が高い人